Packt+ | Advance your knowledge in tech

Explore Products

Best Sellers

New Releases

Books

Videos

Audiobooks

Free Learning

Machine Learning Algorithms

You're reading from Machine Learning Algorithms A reference guide to popular algorithms for data science and machine learning

Product type Paperback

Published in Jul 2017

Publisher Packt

ISBN-13 9781785889622

Length 360 pages

Edition 1st Edition

Languages

Python

Tools

Processing

Concepts

Data Science

Author (1):

Giuseppe Bonaccorso

View More author details

Table of Contents (16) Chapters

Preface

1. A Gentle Introduction to Machine Learning FREE CHAPTER

2. Important Elements in Machine Learning

3. Feature Selection and Feature Engineering

4. Linear Regression

5. Logistic Regression

6. Naive Bayes

7. Support Vector Machines

8. Decision Trees and Ensemble Learning

9. Clustering Fundamentals

10. Hierarchical Clustering

11. Introduction to Recommendation Systems

12. Introduction to Natural Language Processing

13. Topic Modeling and Sentiment Analysis in NLP

14. A Brief Introduction to Deep Learning and TensorFlow

15. Creating a Machine Learning Architecture

Linear support vector machines

Let's consider a dataset of feature vectors we want to classify:

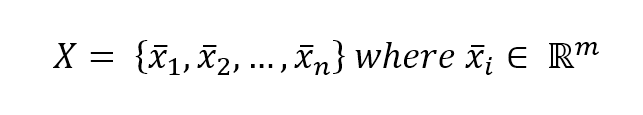
For simplicity, we assume it as a binary classification (in all the other cases, it's possible to use automatically the one-versus-all strategy) and we set our class labels as -1 and 1:

Our goal is to find the best separating hyperplane, for which the equation is:

In the following figure, there's a bidimensional representation of such a hyperplane:

In this way, our classifier can be written as:

In a realistic scenario, the two classes are normally separated by a margin with two boundaries where a few elements lie. Those elements are called support vectors. For a more generic mathematical expression, it's preferable to renormalize our dataset so that the support vectors will lie on two hyperplanes with equations:

In the following figure, there's an example with two support vectors. The dashed line is the original separating hyperplane:

Our goal is to maximize the distance between these two boundary hyperplanes...

The rest of the chapter is locked

Register for a free Packt account to unlock a world of extra content!

A free Packt account unlocks extra newsletters, articles, discounted offers, and much more. Start advancing your knowledge today.

Unlock this book and the full library FREE for 7 days

Get unlimited access to 7000+ expert-authored eBooks and videos courses covering every tech area you can think of

Start free trial

Renews at $19.99/month. Cancel anytime

Other recommended products

Related to this chapter

Machine Learning Algorithms

Machine Learning Algorithms

Machine learning explores the study and construction of algorithms that can learn from and make predictions on data. This book will act as an entry point for anyone who wants to make a career in Machine Learning. It covers algorithms like Linear regression, Logistic Regression, SVM, Naïve Bayes, K-Means, Random Forest, and Feature engineering.

Aug 2018 17h 24m

Hands-On Unsupervised Learning with Python

Hands-On Unsupervised Learning with Python

Unsupervised learning is a key required block in both machine learning and deep learning domains. You will explore how to make your models learn, grow, change, and develop by themselves whenever they are exposed to a new set of data. With this book, you will learn the art of unsupervised learning for different real-world challenges.

Feb 2019 12h 52m

Mastering Machine Learning Algorithms

Mastering Machine Learning Algorithms

A new second edition of the bestselling guide to exploring and mastering the most important algorithms for solving complex machine learning problems, updated to include Python 3.8 and TensorFlow 2.x as well as the latest in new algorithms and techniques.

Jan 2020 26h 36m

Mastering Machine Learning Algorithms

Mastering Machine Learning Algorithms

This book is your guide to quickly get to grips with the most widely used machine learning algorithms. As a data science professional, this book will help you design and train better machine learning models to solve a variety of complex problems, and make the machine learn your requirements.

May 2018 19h 12m

Machine Learning with scikit-learn Quick Start Guide

Machine Learning with scikit-learn Quick Start Guide

Scikit-learn is a robust machine learning library for the Python programming language. It provides a set of supervised and unsupervised learning algorithms. This book is the easiest way to learn how to deploy, optimize and evaluate all the important machine learning algorithms that scikit-learn provides.

Oct 2018 5h 44m

scikit-learn Cookbook

scikit-learn Cookbook

scikit-learn has evolved as a robust library for machine learning applications in python with support for a wide range of supervised and unsupervised learning algorithms. This edition brings to you the various enhancements to its model implementations, API and bug fixes in the latest major release of scikit-learn to support Python. This book covers easy to follow recipes right from mathematical operations to implementing various supervised, unsupervised and deep learning algorithms with scikit-learn. Get practical hands-on knowledge to implement various models and algorithms like Multi-Layer Perceptrons, time-series split, MAE criterion for regression, criteria for gradient boosting, Classifier, Regressor, and much more.

Nov 2017 12h 28m

Ensemble Machine Learning Cookbook

Ensemble Machine Learning Cookbook

This book uses a recipe-based approach to showcase the power of machine learning algorithms to build ensemble models using Python libraries. Through this book, you will be able to pick up the code, understand in depth how it works, execute and implement it efficiently. This will be a desk reference to implement a wide range of tasks and solve the common and uncommon problems in ensemble machine learning domain.

Jan 2019 11h 12m

Supervised Machine Learning with Python

Supervised Machine Learning with Python

A supervised learning task infers a function from flagged training data and maps an input to an output based on sample input-output pairs. In this book, you will learn various machine learning techniques (such as linear and logistic regression) and gain the practical knowledge you need to quickly and powerfully apply algorithms to new problems.

May 2019 5h 24m

Hands-On Ensemble Learning with Python

Hands-On Ensemble Learning with Python

Ensemble learning can provide the necessary methods to improve the accuracy and performance of existing models. In this book, you'll understand how to combine different machine learning algorithms to produce more accurate results from your models.

Jul 2019 9h 56m

Python Data Mining Quick Start Guide

Python Data Mining Quick Start Guide

This book is an introduction to data mining and its practical demonstration of working with real-world data sets. With this book, you will be able to extract useful insights using common Python libraries. You will also learn key stages like data loading, cleaning, analysis, visualization to build an efficient data mining pipeline.

Apr 2019 6h 16m

Mastering Machine Learning with scikit-learn

Mastering Machine Learning with scikit-learn

This book examines machine learning models including k-nearest neighbors, logistic regression, naive Bayes, random forests, and support vector machines. You will work through document classification, image recognition, and other example problems.

Jul 2017 8h 28m

Hands-On Machine Learning with scikit-learn and Scientific Python Toolkits

Hands-On Machine Learning with scikit-learn and Scientific Python Toolkits

This book covers the theory and practice of building data-driven solutions. Includes the end-to-end process, using supervised and unsupervised algorithms. With each algorithm, you will learn the data acquisition and data engineering methods, the apt metrics, and the available hyper-parameters. You will learn how to deploy the models in production.

Jul 2020 12h 48m

Personalised recommendations for you

Based on your interests and search pattern

Modern Computer Vision with PyTorch

Modern Computer Vision with PyTorch

This book provides a hands-on approach to solving over 30 prominent real-world computer vision problems using PyTorch 2.x on actual datasets. Here you'll learn to build a neural network from scratch and optimize hyperparameters, perform image classification, multi-object detection, segmentation, and more. You'll also explore facial expression manipulation and combining CV with NLP and RL techniques, build generative AI applications, and take your model to production on AWS. By the end of this book, you'll master modern NN architectures and confidently solve real-world CV problems.

Jun 2024 24h 52m

Data Governance Handbook

Data Governance Handbook

This book provides a highly focused view of real business outcomes powered by data governance, that resonate with non-data executives such as CFOs and CEOs. You'll also find useful insights into how to implement data governance initiatives.

May 2024 13h 8m

Data Engineering with Databricks Cookbook

Data Engineering with Databricks Cookbook

This book shows you how to use Apache Spark, Delta Lake, and Databricks to build data pipelines, manage and transform data, optimize performance, and more. Additionally, you'll implement DataOps and DevOps practices, and orchestrate data workflows.

May 2024 14h 36m

Azure Data Engineer Associate Certification Guide

Azure Data Engineer Associate Certification Guide

Unlock the power of Azure data engineering with this certification guide, elevating your skills in data processing, storage, and security with the help of practical insights, hands-on exercises, and the latest advancements.

May 2024 18h 16m

Microsoft Power BI Cookbook

Microsoft Power BI Cookbook

Microsoft Power BI is the most sought-after platform for BI professionals' visualization needs. Explore the latest Power BI features, future AI enhancements, and integration with other Power Platform tools via new recipes in this updated edition.

Jul 2024 19h 56m

Python Data Cleaning Cookbook

Python Data Cleaning Cookbook

The book shows you how to clean, wrangle, and view data from multiple perspectives, including dataset and column attributes. You will cover common and not-so-common challenges that are faced while cleaning messy data for complex situations and learn to manipulate data to get it down to a form that can be useful for making the right decisions.

May 2024 16h 12m

Microsoft Azure AI Fundamentals AI-900 Exam Guide

Microsoft Azure AI Fundamentals AI-900 Exam Guide

This AI-900 study guide will help you prepare and practice for the certification exam. You'll delve into AI workloads, ML principles, computer vision, NLP, knowledge mining, and generative AI using Azure cloud services.

May 2024 9h 36m

Using Stable Diffusion with Python

Using Stable Diffusion with Python

This book shows you how to use Python to control Stable Diffusion and generate high-quality images. In addition to covering the basic usage of the diffusers package, the book provides solutions for extending the package for more advanced purposes.

Jun 2024 11h 44m

Getting Started with DuckDB

Getting Started with DuckDB

This hands-on book teaches you to analyze large datasets with blazing speed and ease. You will learn how to use DuckDB to quickly load, query, transform, analyze, and visualize data effectively through a series of practical examples.

Jun 2024 12h 44m

Databricks Certified Associate Developer for Apache Spark Using Python

Databricks Certified Associate Developer for Apache Spark Using Python

This guide gets you ready for certification with expert-backed content, key exam concepts, and topic reviews. Additionally, you'll be able to make the most of Apache Spark 3.0 to modernize workloads and more using specific tools and techniques.