Simionescu’s function and constrained optimization
At first glance, Simionescu’s function may not look particularly interesting. However, it has a constraint attached to it that makes it intriguing to work with as well as pleasant to look at.
The function is usually evaluated on the search space bounded by [-1.25, 1.25] in each dimension and can be mathematically expressed as follows:
f(x, y) = 0.1xy
Here, the values of x, y are subject to the following condition:
x 2 + y 2 ≤ [1 + 0.2 ⋅ cos(8 ⋅ arctan x _ y )] 2
This constraint effectively limits the values of x and y that are considered valid for this function. The result is depicted in the following contour diagram:
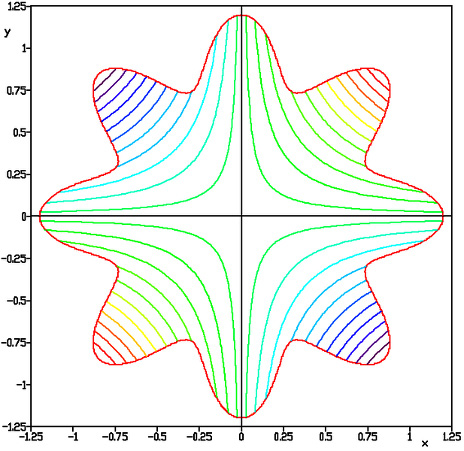
Figure 6.12: Contour diagram of the constrained Simionescu’s function
Source: https://commons.wikimedia.org/wiki/File:Simionescu%27s_function.PNG
Image by Simiprof
The flower-shaped border is...































































