Component-wise operations
Given two vectors, there are several component-wise operations we can perform. These operations will operate on each component of the vector and yield a new vector.
You can add two vectors component wise. Given two n-dimensional vectors  and
and  , addition is defined as follows:
, addition is defined as follows:
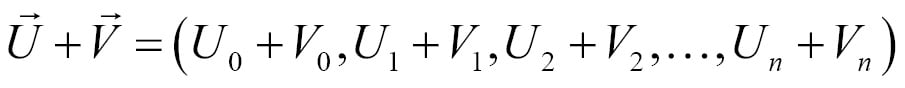
You can also subtract two vectors component wise. Given two n-dimensional vectors  and
and  , subtraction is defined as follows:
, subtraction is defined as follows:
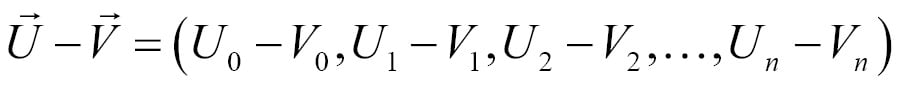
Multiplying two vectors can also be done component wise. There are other ways to multiply two vectors; the dot product or cross product. Both of these alternate methods will be covered later in this chapter. Given two n-dimensional vectors  and
and  , multiplication is defined as follows:
, multiplication is defined as follows:
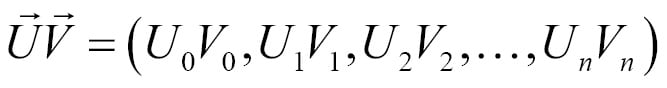
In addition to multiplying two vectors, you can also multiply a vector by a scalar. In this context, a scalar is any real number. Given vector  and scalar S, scalar multiplication is defined as follows:
and scalar S, scalar multiplication is defined as follows:
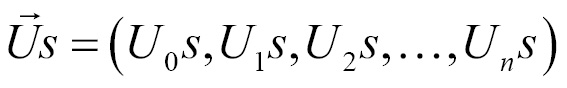
Finally, we can check for vector equality by comparing each component of the vectors being tested. Two vectors are the same only if all of their components are equal.
Getting ready
We're going to implement all of the preceding component-wise operations by overloading the appropriate C++ operators. All of the operators presented in this section can be overloaded in C# as well. In languages that do not support operator overloading, you will have to make these into regular functions.
How to do it…
Follow these steps to override common operators for the vector class. This will make working with vectors feel more intuitive:
- In
vectors.h, add the following function declarations:vec2 operator+(const vec2& l, const vec2& r); vec3 operator+(const vec3& l, const vec3& r); vec2 operator-(const vec2& l, const vec2& r); vec3 operator-(const vec3& l, const vec3& r); vec2 operator*(const vec2& l, const vec2& r); vec3 operator*(const vec3& l, const vec3& r); vec2 operator*(const vec2& l, float r); vec3 operator*(const vec3& l, float r); bool operator==(const vec2& l, const vec2& r); bool operator==(const vec3& l, const vec3& r); bool operator!=(const vec2& l, const vec2& r); bool operator!=(const vec3& l, const vec3& r);
- Create a new C++ source file,
vectors.cpp. Include the following headers in the new file:#include "vectors.h" #include <cmath> #include <cfloat>
- Add a macro for comparing floating point numbers to
vectors.cpp:#define CMP(x, y) \ (fabsf((x)–(y)) <= FLT_EPSILON * \ fmaxf(1.0f, \ fmaxf(fabsf(x), fabsf(y))) \ ) - Add the implementation of vector addition to the
vectors.cppfile:vec2 operator+(const vec2& l, const vec2& r) { return { l.x + r.x, l.y + r.y }; } vec3 operator+(const vec3& l, const vec3& r) { return { l.x + r.x, l.y + r.y, l.z + r.z }; } - Add the implementation of vector subtraction to the
vectors.cppfile:vec2 operator-(const vec2& l, const vec2& r) { return { l.x - r.x, l.y - r.y }; } vec3 operator-(const vec3& l, const vec3& r) { return { l.x - r.x, l.y - r.y, l.z - r.z }; } - Add the implementation for vector multiplication to the
vectors.cppfile:vec2 operator*(const vec2& l, const vec2& r) { return { l.x * r.x, l.y * r.y }; } vec3 operator*(const vec3& l, const vec3& r) { return { l.x * r.x, l.y * r.y, l.z * r.z }; } - Add the implementation for scalar multiplication to the
vectors.cppfile:vec2 operator*(const vec2& l, float r) { return { l.x * r, l.y * r }; } vec3 operator*(const vec3& l, float r) { return { l.x * r, l.y * r, l.z * r }; } - Finally, add the implementation for vector equality to the
vectors.cppfile. This is where the compare macro we created in step 3 comes in:bool operator==(const vec2& l, const vec2& r) { return CMP(l.x, r.x) && CMP(l.y, r.y); } bool operator==(const vec3& l, const vec3& r) { return CMP(l.x, r.x) && CMP(l.y, r.y) && CMP(l.z, r.z); } bool operator!=(const vec2& l, const vec2& r) { return !(l == r); } bool operator!=(const vec3& l, const vec3& r) { return !(l == r); }
How it works…
What these components-wise operations are doing might not be obvious from the definitions and code provided alone. Let's explore the component-wise operations of vectors visually.
Addition
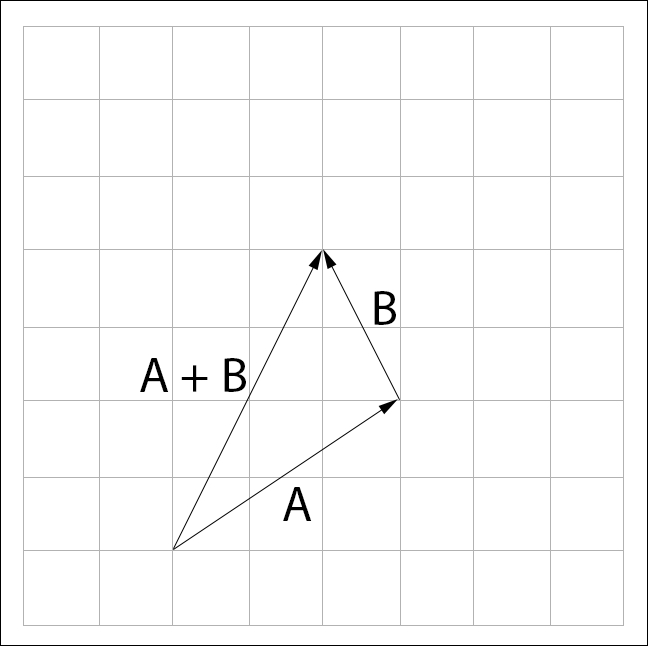
Every vector describes a series of displacements. For example, the vector (2, 3) means move two units in the positive X direction and three units in the positive Y direction. We add vectors by following the series of displacements that each vector represents. To visualize this, given vectors  and
and  , draw them so the head of
, draw them so the head of  touches the tail of
touches the tail of  The result of the addition is a new vector spanning from the tail of
The result of the addition is a new vector spanning from the tail of  to the head of
to the head of  :
:
Subtraction
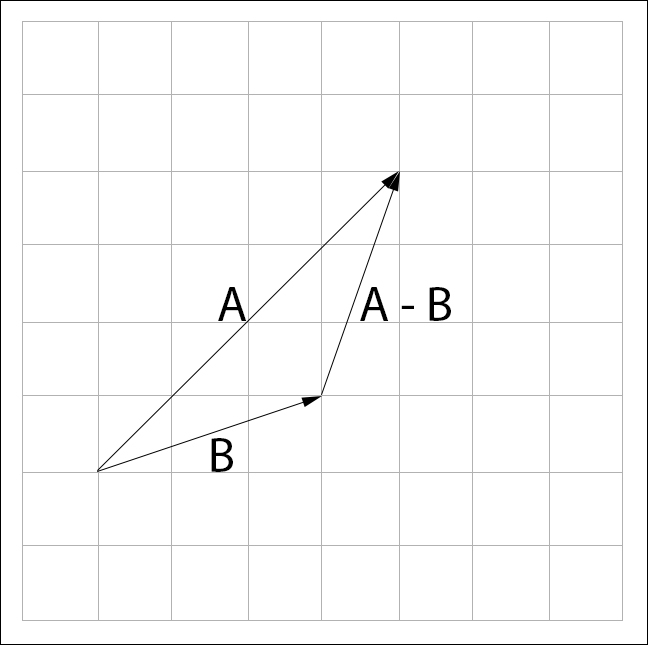
Subtraction works the same way as addition. We have to follow the negative displacement of vector  starting from vector
starting from vector  . To visually subtract vectors
. To visually subtract vectors  and
and  , draw
, draw  and
and  with their tails touching. The result of the subtraction is a vector spanning from the head of
with their tails touching. The result of the subtraction is a vector spanning from the head of  to the head of
to the head of  :
:
A more intuitive way to visualize subtraction might be to think of it as adding negative  to
to , like so;
, like so;  . If we represent the subtraction like this, visually we can follow the rules of addition:
. If we represent the subtraction like this, visually we can follow the rules of addition:
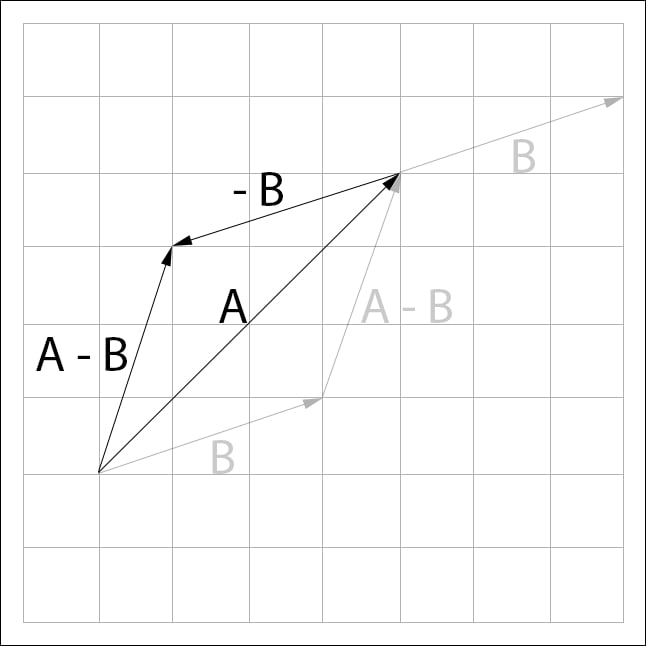
In the above image, the vector  appears multiple times. This is to emphasize that the position of a vector does not matter. Both of the
appears multiple times. This is to emphasize that the position of a vector does not matter. Both of the  vectors above represent the same displacement!
vectors above represent the same displacement!
Multiplication (Vector and Scalar)
Multiplying a vector by a scalar will scale the vector. This is easy to see when we visualize the result of a multiplication. The scalar multiplication of a vector will result in a uniform scale, where all components of the vector are scaled by the same amount. Multiplying two vectors on the other hand results in a non-uniform scale. This just means that each component of the vector is scaled by the corresponding component of the other vector:
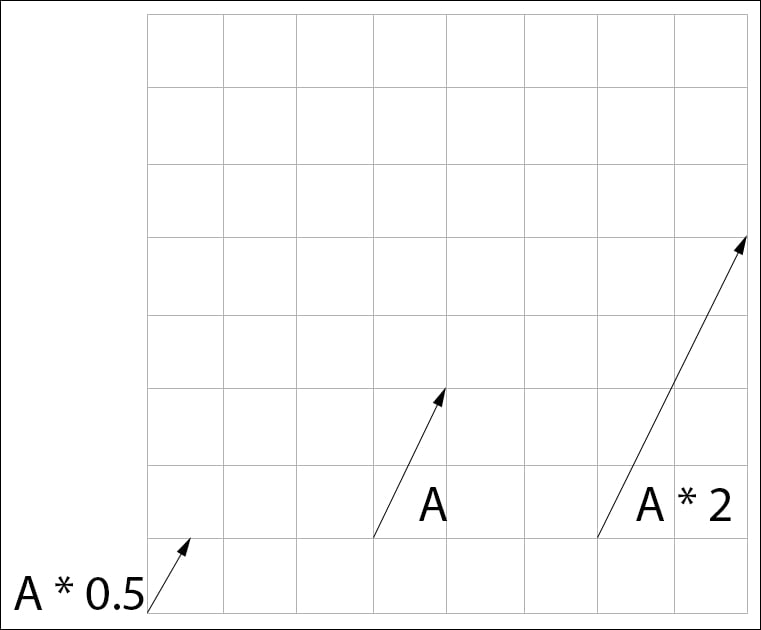
Comparison
Comparing vectors is a component-wise operation. If every component of each vector is the same, the vectors are equal. However, due to floating point error we can't compare floats directly. Instead, we must do an epsilon comparison. Epsilon tests commonly fall in one of two categories: absolute tolerance and relative tolerance:
#define ABSOLUTE(x, y) (fabsf((x)–(y)) <= FLT_EPSILON) #define RELATIVE(x, y) \ (fabsf((x) – (y)) <= FLT_EPSILON * Max(fabsf(x), fabsf(y)))
The absolute tolerance test fails when the numbers being compared are large. The relative tolerance test fails when the numbers being compared are small. Because of this, we implemented a tolerance test with the CMP macro that combines the two. The logic behind the CMP macro is described by Christer Ericson at www.realtimecollisiondetection.net/pubs/Tolerances.
There's more…
It's desirable to make vectors easy to construct in code. We can achieve this by adding default constructors. Each vector should have two constructors: one that takes no arguments and one that takes a float for each component of the vector. We do not need a copy constructor or assignment operator as the vec2 and vec3 structures do not contain any dynamic memory or complex data. The pair of constructors for the vec2 structure will look like this:
vec2() : x(0.0f), y(0.0f) { }
vec2(float _x, float _y) : x(_x), y(_y) { }The vec3 constructors will look similar, it adds an additional component. The constructors for the vec3 structure will look like this:
vec3() : x(0.0f), y(0.0f), z(0.0f) { }
vec3(float _x, float _y, float _z) : x(_x), y(_y), z(_z) { }




























































