Matrix operations
Let’s learn how to use nested lists to perform basic matrix operations. Although many developers use NumPy to perform matrix operations, it’s very useful to learn how to manipulate matrices using straight Python. First, you will add two matrices in Python. Matrix addition requires both matrices to have the same dimensions; the results will also be of the same dimensions.
In the next exercise, you will perform matrix operations.
Exercise 27 – implementing matrix operations (addition and subtraction)
In this exercise, you will use the matrices in the following figures:
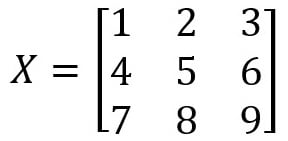
Figure 2.7 – Matrix data for the X matrix

Figure 2.8 – Matrix data for the Y matrix
Now, let’s add and subtract the X and Y matrices using Python.
The following steps will enable you to complete this exercise:
- Open a new Jupyter Notebook.
- Create two nested lists,
XandY, to store the values:X = [[1,2,3],[4,5,6],[7,8,9]]
Y = [[10,11,12],[13,14,15],[16,17,18]]
- Initialize a 3 x 3 zero matrix called
resultas a placeholder:# Initialize a result placeholder
result = [[0,0,0],
[0,0,0],
[0,0,0]]
- Now, implement the algorithm by iterating through the cells and columns of the matrix:
# iterate through rows
for i in range(len(X)):
# iterate through columns
for j in range(len(X[0])):
result[i][j] = X[i][j] + Y[i][j]
print(result)
As you learned in the previous section, first, you iterate the rows in the X matrix, then iterate the columns. You do not have to iterate the Y matrix again because both matrices are of the same dimensions. The result of a particular row (denoted by i) and a particular column (denoted by j) equals the sum of the respective row and column in the X and Y matrices.
The output will be as follows:
[[11, 13, 15], [17, 19, 21], [23, 25, 27]]
- You can also perform subtraction using two matrices using the same algorithm with a different operator. The idea behind this is the same as in Step 3, except you are doing subtraction. You can implement the following code to try out matrix subtraction:
X = [[10,11,12],[13,14,15],[16,17,18]]
Y = [[1,2,3],[4,5,6],[7,8,9]]
# Initialize a result placeholder
result = [[0,0,0],
[0,0,0],
[0,0,0]]
# iterate through rows
for i in range(len(X)):
# iterate through columns
for j in range(len(X[0])):
result[i][j] = X[i][j] - Y[i][j]
print(result)
Here is the output:
[[9, 9, 9], [9, 9, 9], [9, 9, 9]]
In this exercise, you were able to perform basic addition and subtraction using two matrices. In the next section, you will perform multiplication on matrices.
Matrix multiplication operations
Let’s use nested lists to perform matrix multiplication for the two matrices shown in Figures 2.9 and 2.10:
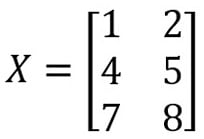
Figure 2.9 – The data of the X matrix
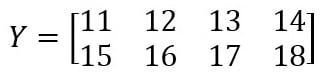
Figure 2.10 – The data of the Y matrix
For matrix multiplication, the number of columns in the first matrix (X) must equal the number of rows in the second matrix (Y). The result will have the same number of rows as the first matrix and the same number of columns as the second matrix. In this case, the resulting matrix will be a 3 x 4 matrix.
Exercise 28 – implementing matrix operations (multiplication)
In this exercise, your end goal will be to multiply two matrices, X and Y, and get an output value. The following steps will enable you to complete this exercise:
- Open a new Jupyter notebook.
- Create two nested lists,
XandY, to store the value of theXandYmatrices:X = [[1, 2], [4, 5], [3, 6]]
Y = [[1,2,3,4],[5,6,7,8]]
- Create a zero-matrix placeholder to store the result:
result = [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
- Implement the matrix multiplication algorithm to compute the result:
# iterating by row of X
for i in range(len(X)):
# iterating by column by Y
for j in range(len(Y[0])):
# iterating by rows of Y
for k in range(len(Y)):
result[i][j] += X[i][k] * Y[k][j]
You may have noticed that this algorithm is slightly different from the one you used in Step 3 of Exercise 27 – implementing matrix operations (addition and subtraction). This is because you need to iterate the rows of the second matrix, Y, as the matrices have different shapes, which is what is mentioned in the preceding code snippet.
- Now, print the final result:
for r in result:
print(r)
Let’s look at the output:

Figure 2.11 – Output of multiplying the X and Y matrices
Note
To review the packages that data scientists use to perform matrix calculations, such as NumPy, check out https://docs.scipy.org/doc/numpy/.
In the next section, you will work with and learn about a new data structure: Python dictionaries.
































































