A survey of sets
So far, in this chapter, we have covered lists, dictionaries, and tuples. Now, let’s look at sets, which are another type of Python data structure.
Sets are a relatively new addition to the Python collection type. They are unordered collections of unique and immutable objects that support operations mimicking mathematical set theory. Since sets do not allow multiple occurrences of the same element, they can be used to effectively prevent duplicate values.
A set is a collection of objects (called members or elements). For instance, you can define set A as containing even numbers between 1 to 10, and it will contain {2,4,6,8,10}; set B can contain odd numbers between 1 to 10, and it will contain {1,3,5,7,9}.
The following figure shows a visual of two sets without overlapping values:
Figure 2.19 – Set A and Set B – each set contains a unique, distinct value
In the following exercise, you will work with sets in Python.
Exercise 33 – using sets in Python
In this exercise, you will practice working with sets in Python:
- Open a Jupyter notebook.
- Initialize a set using the following code. You can pass in a list to initialize a set or use curly brackets, as follows:
s1 = set([1,2,3,4,5,6])
print(s1)
s2 = {1,2,2,3,4,4,5,6,6}print(s2)
s3 = {3,4,5,6,6,6,1,1,2}print(s3)
The output is as follows:
{1, 2, 3, 4, 5, 6}
{1, 2, 3, 4, 5, 6}
{1, 2, 3, 4, 5, 6}
Here, you can see that the set is unique and unordered, so duplicate items and the original order are not preserved.
- Enter the following code in a new cell:
s4 = {'martha graham, 'alivin ailey, 'isadora duncan'}print(s4)
You can also initialize a set using curly brackets directly.
The output is as follows:
{'martha graham', 'alvin ailey', 'isadora duncan'}
- Sets are mutable. Type the following code, which shows how to add a new item,
pineapple, to an existing set,s4:s4.add('katherine dunham')print(s4)
The output is as follows:
{'martha graham', 'alvin ailey', 'isadora duncan'}
In this exercise, you were introduced to sets in Python. In the next section, you will dive in a bit deeper and understand the different set operations that Python offers.
Set operations
Sets support common operations such as unions and intersections. A union operation returns a single set that contains all the unique elements in both sets A and B; an intersect operation returns a single set that contains unique elements that belong to set A and also belong to set B at the same time. Let’s look at the union operation in the following figure:
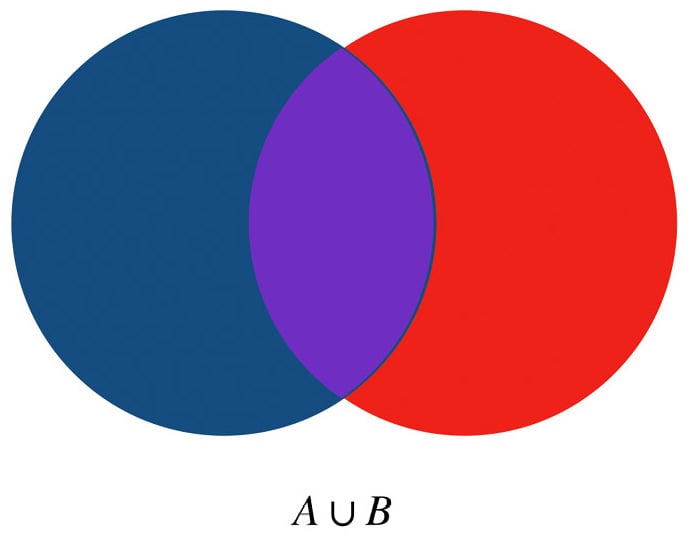
Figure 2.20 – Set A in union with Set B
The following figure represents the intersect operation:
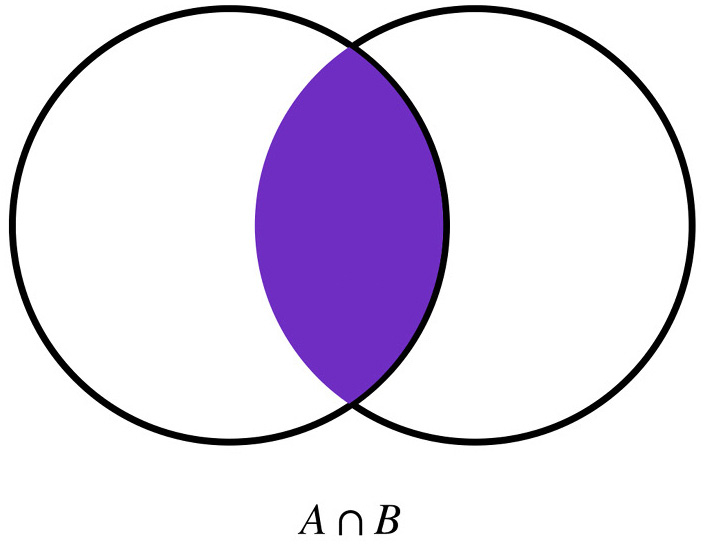
Figure 2.21 – Set A intersects with Set B
Now, let’s implement these set operations in Python in the following exercise.
Exercise 34 – implementing set operations
In this exercise, we will be implementing and working with set operations:
- Open a new Jupyter notebook.
- In a new cell, type the following code to initialize two new sets:
s5 = {1,2,3,4}s6 = {3,4,5,6} - Use the
|operator or theunionmethod for a union operation:print(s5 | s6)
print(s5.union(s6))
The output is as follows:
{1, 2, 3, 4, 5, 6}
{1, 2, 3, 4, 5, 6}
- Now, use the
&operator or theintersectionmethod for anintersectionoperation:print(s5 & s6)
print(s5.intersection(s6))
The output is as follows:
{3, 4}
{3, 4}
- Use the
–operator or thedifferencemethod to find the difference between two sets:print(s5 - s6)
print(s5.difference(s6))
The output is as follows:
{1, 2}
{1, 2}
- Now, enter the
<=operator or theissubsetmethod to check if one set is a subset of another:print(s5 <= s6)
print(s5.issubset(s6))
s7 = {1,2,3}s8 = {1,2,3,4,5}print(s7 <= s8)
print(s7.issubset(s8))
The output is as follows:
False
False
True
True
The first two statements will return false because s5 is not a subset of s6. The last two statements will return True because s5 is a subset of s6. Note that the <= operator is a test for the subset. A proper subset is the same as a general subset, except that the sets cannot be identical. You can try it out in a new cell with the following code.
- Check whether
s7is a formal subset ofs8, and check whether a set can be a proper subset of itself by entering the following code:print(s7 < s8)
s9 = {1,2,3}s10 = {1,2,3}print(s9 < s10)
print(s9 < s9)
The output is as follows:
True
False
False
Here, we can see that s7 is a proper subset of s8 because there are other elements in s8 apart from all the elements of s7. However, s9 is not a subset of s10 because they are identical. Therefore, a set is not a proper subset of itself.
- Now, use the
>=operator or theissupersetmethod to check whether one set is the superset of another. Try this using the following code in another cell:print(s8 >= s7)
print(s8.issuperset(s7))
print(s8 > s7)
print(s8 > s8)
The output is as follows:
True
True
True
False
The first three statements will return True because s8 is the superset of s7 and is also a proper superset of s7. The last statement will return false because no set can be a proper superset of itself.
Having completed this exercise, you now know that Python sets are useful for efficiently preventing duplicate values and are suitable for common math operations such as unions and intersections.
Note
After all the topics covered so far, you may think that sets are similar to lists or dictionaries. However, sets are unordered and do not map keys to values, so they are neither a sequence nor a mapping type; they are a type by themselves.

































































