Memoization with Fibonacci

Like factorials, Fibonacci is another one of those easy-to-explain problem statements that can be used to demonstrate a language's capabilities in a simple and easy to understand manner. A Fibonacci series is written as follows:

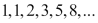
It can also be written as a recurrence:

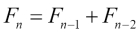
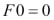
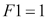
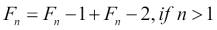
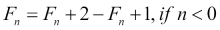
Now that you know what factorials are, a recursive Fibonacci implementation comes very naturally as follows:

let rec fibonacci n =
  if n <= 2 then 1
  else fibonacci (n - 1) + fibonacci (n - 2)

However, based on the earlier factorial solution, you quickly realize that this is indeed not tail-optimized, and will result in a stack overflow. This is due to pushing of pointers in the stack. Applying the same pattern as for the factorial, by using an external function fibonacci and internal recursive function fibonacci_TailRecursive, the resulting tail-optimized method can be written as follows:

let fibonacci_TailRecursive n = 
    let rec fibonacciX (n, x, y) =
       if (n = 0I) then x
       else...