Maintainability is one of the key non-functional requirements when it comes to code upkeep. Software complexity is a deterrent for feature additions, bug fixes, reusability, and refactoring. A well-structured program is not only easy to maintain, but also easy to debug and reuse. In Why Functional Programming Matters - Research topics in functional programming, John Huges argues that modularity is key to effective software maintainability, and modularity means more than mere code segmentation. Decomposing a technology or business problem into smaller segments, and then integrating these smaller problems to build a solution, promotes modular and reusable development practices. Code must be usable before it is reusable; the higher order functions and non-strict (lazy) evaluation of functional programming help build smaller, readable, easily testable, and generic modules.

Functional programing provides abstraction but it is relatively different from the hierarchical facet which we are used to seeing in the object oriented paradigm. In contrast with the object oriented tenet of abstraction, functional abstraction hides how the code executes, and provides a protected logical environment which supports referential transparency, that is, programming without side effects. This lets the developer focus on the results based on the statement provided. Functional code is a declaration that describes the results that a developer is trying to achieve, instead of focusing on the steps to get there.

Functional syntax tends to be less verbose and more terse than its imperative or object oriented counterpart. The terseness keeps KLOC low and often results to the improved developer productivity. In terms of productivity, since functional programming promotes and encourages rapid prototyping, it benefits building and testing out proof of concept implementations. This results in code that has more brevity, is more resilient to change, and has fewer bugs.

Even though this is not strictly a feature of functional programming, several cross-cutting concerns come standard along with most functional programming languages. These include protected environments, pattern matching, tail-call optimization, immutable data structures, and garbage collection.

If you have written multi-threaded code, you'd know that debugging the concurrency issues in a multi-threaded environment is difficult to say the least. Arguably, one of the best features of functional programming is thread safety through immutability. The notion of concurrent collections in modern programming languages has its roots in functional programming. The design and use of immutable data structures prevents the process from running into race conditions and therefore does not present a need for explicit locking, semaphores, and mutex programs. This also helps in parallelization, one of the unrealized promises of functional programming.

In this book, we will discuss these and various other functional programming features in detail, especially in context of F#. As a reader who is potentially familiar with either object oriented or imperative programming, you will enjoy the use of fluent-interface methods, lazy and partial evaluation, currying and memoization, and other unique and interesting concepts that make your life as a developer more fulfilling, and easier too.

With the advent of a multi-paradigm language with functional programming support such as Lisp in 1958 by John McCarthy, the functional paradigm gained mainstream exposure. Due to its multi-paradigm nature, there is a debate around Lisp being a pure functional programming language. However, Scheme, one of the Lisp dialects which didn't appear till 1975, tends to favor the functional style. The salient features of this style includes use of tail recursion and continuations to express control flow.

Furthermore, various other functional languages were developed in academia, mostly in the areas of mathematical sciences for theorem proving. ML (meta-language) by Robin Milner et al of University of Edinburgh (early 1970s) is a prime example of a programming language used to first implement the Hindley–Milner type inference system. This simply typed polymorphic lambda calculus language was later adapted to build StandardML, Caml, and OCaml, unifying functional, OOP, and imperative programming paradigms. Haskell emerged in 1990 by Simon Jones et al as a purely functional programming language. Haskell supports lazy evaluation, non-strict semantics, and strong static typing. Haskell is named after the logician Haskell Curry. Not surprisingly, Currying is the functional approach to deconstructing a tuple into evaluating a sequence of functions. It allows us to deconstruct a function that takes multiple arguments into an equivalent sequence of sub-functions that are evaluated, one argument at a time. We will explore currying further in the book.

F#, a product of Don Syme, and Microsoft Research, surfaced in 2005 as a modern multi-paradigm functional programming language. F# originates from ML and has been influenced by OCaml, C#, Python, Haskell, Scala, and Erlang. F# Software Foundation (FSSF) defines the language as follows:

With an open source compiler, library, and toolset, F# is a multi-paradigm language for the .NET platform with support for multiple operating systems via Mono. It supports functional, object oriented, imperative, and explorative programming paradigms. Software developers who specialize in Microsoft platform and tools can easily learn to take advantage of this new language's functional and object-oriented features. This allows them to use their existing skills, find new productivity gains, and leverage new programming design approaches that cannot be easily expressed in objects alone.

We will be the first to admit that functional programming can be scary for those accustomed to the object oriented and imperative style of coding. While functional programming can lead to some mind-bending coding, the fundamentals are quite straightforward. If you find yourself lost in lambdas, rest assured that it takes everyone some time to master these expressions. Even though the primary focus of this book is not F# programming but rather data structures, we will start by introducing some of the F# language tenets to help get the reader up-to-speed.

The syntactical terseness of a functional language like F# can have an adverse effect on the reader; since functional programming is characterized by its concise coding style, brevity, and explicit modeling, this can be hard for those familiar with the verbose algorithmic style of OO and imperative languages. Rest assured, F# also offers a rich set of object oriented features and its integration with other .NET languages such as C#.NET and VB.NET is nearly seamless.

No book is complete without some quintessential Hello World examples. So here it is:

printfn "Hello World";;

Yes, this is all you need. Notice the terseness, simplicity, and lack of clutter. Now let's run this in the F# interactive environment. In order to run it, you would need to have ";;" at the end of the statement. We will provide more details on this interactive environment setup later in Chapter 2, Now Lazily Get Over It, Again.

This is the response that you see when you run the preceding line of code. It is a minimal viable example; however these attributes of simplicity, terseness, and simplification extend beyond HelloWorld samples as you will see.

Let's look at a simple function, square. You can write a function in F# as follows:

let square = fun n -> n * n

Or you can write it in a simpler syntax like the next one. Notice the first-class citizenship in action here:

let square n = n * n

When this function is executed in F# interactive, you can immediately see the results upon invocation as in the following screenshot:

Even though this book is not intended to be an absolute beginner's primer to F#, if you are new to F# there are certain language fundamentals you must know in order to maximize your learning from this book. Following is a quick F# refresher on basic language constructs, keywords, and salient syntactical features that you will find useful during the course of reading this book Several of these items, especially those related to data-structures, are discussed in greater detail in the following chapters. You can download all these examples and source code from the book GitHub repository at https://github.com/adnanmasood/Learning-fsharp.

F# is a statically typed language, that is, types of the variables are known at compile time. Like all other static type languages, F# uses a type inference to resolve the variable type. F# comes with standard data types such as byte, sbyte, int16, uint16, int, uint, int64, uint64, native int, unsigned native int, float or double, float32, decimal, and bignum (System.Numerics.BigInteger). A few simple declarations with appropriate suffixes can be seen as follows:

let byte b = 10uy
let sbyte sb = -128y
let int16 i = -100s
let uint16 ui = 100us
let int = -42
let uint = 0x42u
let int64 = 238900L
let uint64 = 2,660,000,000UL
let float f = 3.14159265359
let double db = 2.718281828459045
let float32 f32 = 2.7182818
let decimal d = 3.14159265358979323846264338
let bignum gogol = 10I ** 100
let string = "nà, méi guānxi"

Similar to standard CLR data types, F# also uses the standard mathematical operators such as 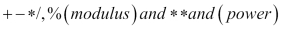. Logical operators 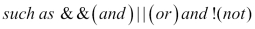are supported along with mathematical functions such as 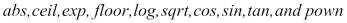. A detailed F# language reference, including Symbol and Operator Reference, can be found at http://msdn.microsoft.com/en-us/library/dd233228.aspx.

At this time, we would also like to briefly introduce you to one of the highly useful features of F# IDE, the REPL. REPL (Read–Eval–Print Loop) is an interactive language shell to take expression inputs, evaluate, and provide output to the users. REPL allows developers to interact with the language easily and to invoke and test expressions in real-time before writing the entire program. FSI (F Sharp Interactive) is the REPL implementation in F#. You will read more about installing and configuring FSI in Chapter 2, Now Lazily Get Over It, Again. For now you can use the command line version of FSI by invoking it directly in a console:

C:\Program Files\Microsoft F#\v4.0\fsi.exe

You can also use the #help;; directive to list other directives inside FSI.

You will see the let binding being used quite frequently for declaring variables, functions, and so on. Functions put functions in functional programming and hence, they are ubiquitous. Technically speaking, F# doesn't have any statements, it only has expressions. The following is a simple example of a function:

let cubeMe x = x * x * x;;

Instead of explicitly returning a value, F# uses a succinct syntax of returning the value of the expression last evaluated.

val cubeMe : x:int -> int
> > cubeMe 9;;
val it : int = 729

Recursive functions are defined using the keyword rec. Here is a simple implementation of a recursive Fibonacci function:

let rec fib n =
  if n <= 2 then 1
  else fib (n - 1) + fib (n - 2)

The preceding code for the Fibonacci method takes one parameter as an input. However, a function can have more than one parameters following the same code.

let Mult x y = x * y ;;

Type inference in F# is an important construct to remember. For instance, in the case of the multiplication function in the preceding line of code, F# assumes the type inference of the arguments as int. A hint can be provided to specify the appropriate data type.

let Mult (x: float) (y: float) = x * y ;;

Nested or anonymous functions are now commonplace in languages such as C# and Java. These are the special functions that reside inside another function and are not visible from an outside scope. For instance, refer to the following code snippet:

let areaOfCircle r = 
  let square r = r * r
  System.Math.PI * square r;;

However the preceding function will fail upon execution without a hint. We will see the following error on screen:

error FS0001: This expression was expected to have type   float    but here has type    int    

But the same method will work just fine if the specified data type is passed as float.

> areaOfCircle 8.0;;
val it : float = 201.0619298

Moreover, you cannot call the inner function directly. That is why the direct call to the square method will return the following error:

square 10;;
^^^^^^
error FS0039: The value or constructor 'square' is not defined

The conditionals are fundamental to any programming language. F# provides a great pattern-matching scheme along with traditional if...else expressions. The following is a simple if...else check:

let Mod10 n = 
  if n % 10 = 0 then
    printfn "Number ends in 0"
  else
    printfn "Number does not end in zero";;

The print expression will return a value. You can also see the use of elif which is used as a shortcut for else if.

Tuples are now part of a standard CLR system, but most of us remember the struggle before tuples. Tuples are the containers for potentially different types, as seen in the following code:

let t = ("cats", "dogs", System.Math.PI, 42, "C#", "Java");;
val t : string * string * float * int * string * string = ("cats", "dogs", 3.141592654, 42, "C#", "Java")

Speaking of collections, arrays in F# are mutable, fixed-sized sequences. Arrays are fixed in size and zero-indexed, with the elements encapsulated within [| … |] and separated by a semi-colon.

let GuardiansOfGalaxy = [| "Peter Quill"; "Gamora"; "Drax"; "Groot"; "Rocket"; "Ronan"; "Yondu Udonta"; "Nebula"; "Korath"; "Corpsman Dey";"Nova Prime";"The Collector";"Meredith Quill" |]

The individual elements of the array can be accessed as follows:

let iAmGroot = GuardiansOfGalaxy.[4];
val iAmGroot : string = "Rocket"

This also applies to the strings where you can access an individual element of a string as follows:

let str = "Lǎo péngyǒu, nǐ kànqǐlái hěn yǒu jīngshén."
printfn "%c" str.[9]

Arrays can be created using ranges as follows:

let OneToHundred = [|1..100|];;

They can be sliced using index (arrays are zero base indexed) as seen in the following code:

let TopThree = OneToHundred.[0..2];;

Functions in F# can be applied partially; it gets interesting here. A simple add function can be defined as follows:

let add x y = x + y;;

We can apply it partially to make it add 10 every time. Therefore, the following statement:

(add 10) 4;;

This can be bound as a method name, or a closure to be exact as seen here:

let Add10 = add 10;
val Add10 : (int -> int)

This can be explicitly called like the original method, allowing us to compose complex methods using the basic ones. Here, Add10 is a closure that takes one argument and adds 10 to it as seen in the following code:

Add10 42
> 
val it : int = 52

Closures are functionally defined as a first-class function with free variables that are bound in the lexical environment. In F#, functions are first class members of the programming society; closures encapsulate an environment for pre-bound variables and create a code block. This way we can pre-define some arguments (in this case, 10). Closure promotes reuse and helps in building complex functions from simpler ones.

With functions as the first class citizens, in F# we can create higher order functions, that is, functions upon functions. Higher order functions operate by taking a function as an argument, or by returning a function. Following are two simple functions:

let increament n = n + 1
let divideByTwo n = n / 2

Now we will define a higher order function which applies function upon function:

let InvokeThrice n (f:int->int) = f(f(f(n)))

Now we will use the InvokeThrice function, which will apply the function upon itself three times as defined in the preceding line of code:

let res = InvokeThrice 6 increament
> 
val res : int = 9

In this example, you witnessed the amazing power of declaring functions. A similar approach can be applied to division as follows:

let res = InvokeThrice 80 divideByTwo
> 
val res : int = 10

In the preceding syntax for the InvokeThrice function, you will notice the use of a lambda expression. Lambda expressions are ubiquitous in functional programming. In reality, these expressions are syntactic sugar (directives, shortcuts, or a terse way of defining something) to declare anonymous methods. A lambda expression is created using the fun keyword, that is, function, followed by arguments which are supposed to be passed to the function. This function declaration is then followed by the lambda arrow operator -> and the lambda expression which defines the body of the function. For example, instead of passing the function, I can pass the lambda expression during the InvokeThrice invocation to apply exponential operation (power 3).

let InvokeThrice n (f:double->double) = f(f(f(n)))
let x = InvokeThrice 2.0 (fun n -> n ** 3.0)

val x : double = 134217728.0

Another frequently used F# operator is pipelining |>, which allows us to push arguments onto functions. For example, check the following cubeMe method:

let cubeMe x = x * x * x;;

The preceding method can also be called as cubeMe 3 or 3 |> cubeMe.

The results will be the same. The pipelining operator allows us to do chaining such as:

2 |> cubeMe |> cubeMe |> cubeMe 
> val it : int = 134217728

This comes in handy when you build functional composites.

Mapping is a frequently used operation in functional programming. Map applies functions on a collection, and displays output as a new list, based on the result of this function. For arrays, F# provides a built-in operation called map. The map operation takes two arguments—a function and an array of elements. For example, refer to the following array of integers:

let nums = [|0..99|]

val nums : int [] =
  [|0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 
  //snip
  97; 98; 99|]

The following is the mapping function that will square all the elements in the array, and return a new array:

let squares = 
  nums
  |> Array.map (fun n -> n * n)

When you run the square method on nums, you get the following output:

val squares : int [] =
  [|0; 1; 4; 9; 16; 25; 36; 49; 64; 81; 100; 121; 144; 169; 196; 225; 256; 
//snip
  8649; 8836; 9025; 9216; 9409; 9604; 9801|]

The opposite of the map operation is the fold operation. You can think of the folding operations as aggregations. As seen in the preceding code snippet, map takes a collection of arrays and generates another collection. However, the folding operation takes a collection of arrays as input and returns a single object.

For example, in the next statement, Array.fold takes three arguments—a function, an initial value for the accumulator, and an array. It sums up the squares of all the three parameters and returns the output:

let sum = Array.fold(fun acc n ->  acc + n ) 0 squares 

> val sum : int = 328350

Along with map and fold, filtering is another operation which comes in handy to select and filter elements based on a condition (predicate). In the following example, Array.filter takes an array of last names and folders them based on the length. Any last name longer than 6 characters will be classified as a long name.

let castNames = [| "Hofstadter"; "Cooper"; "Wolowitz"; "Koothrappali"; "Fowler"; "Rostenkowski";  |]

let longNames = Array.filter (fun (name: string) -> name.Length > 6) castNames

The output will be as follows:

val longNames : string [] =
  [|"Hofstadter"; "Wolowitz"; "Koothrappali"; "Rostenkowski"|]

Similar to map, which applies a function on a collection, a zipping function takes two collections and combines them. In the following example we have two lists:

let firstNames = [| "Leonard"; "Sheldon"; "Howard"; "Penny"; "Raj"; "Bernadette"; "Amy" |]
let lastNames = [| "Hofstadter"; "Cooper"; "Wolowitz"; ""; "Koothrappali"; "Rostenkowski"; "Fowler" |]

A zip operation when applied on the array returns their full names:

let fullNames = Array.zip(firstNames) lastNames

Last but not the least, another salient feature of F# language is Lazy or delayed evaluation. These lazy expressions only get evaluated when forced, or when a value is required to be returned. The value then gets memoized (a fancy functional name for caching), and is returned on future recalls. The following is a simple divide method:

let divide x y = 
  printfn "dividing %d by %d" x y
  x / y
val divide : x:int -> y:int -> int

When you invoke the method with the Lazy keyword, the output shows that the value does not get created right away.

let answer = lazy(divide 8 2)
val answer : Lazy<int> = Value is not created.

However, this can be changed by forcing the results by calling answer.Force():

printfn "%d" (answer.Force()) 

> dividing 8 by 2
4
val it : unit = ()

Now upon force invocation, you would see the value was evaluated by calling the function and therefore you also see dividing 8 by 2 getting printed on the FSI console. Upon consecutive calls such as

printfn "%d" (answer.Force())

The output would be as follows:

4
val it : unit = ()

You would not see dividing 8 by 2 getting printed on the FSI console because the value has been computed and memoized. Collections such as sequence are lazy by default, which you will learn in subsequent chapters.

This concludes our whirlwind introduction to the F# programming language; if you are new to F#, you should revise this section a couple of times and run this in the interactive environment to gain familiarity with these fundamental language constructs.

Let's expand upon the preceding example and compare the syntactical differences between F# and C# through another simple example, the sum of a square method. A shorter and elegant looking functional syntax follows:

let square x = x * x
let sumOfSquares n = [1..n] |> List.map square |> List.sum 

Here you see the use of one of F#'s celebrated operators, that is, the |> pipe forward operator. It essentially performs piping operations by passing the results from left the side of the function to the right side, and can be concatenated.

Running this program in F# the interactive console yields the following results for

sumOfSquares 2 

and

sumOfSquares 3 

respectively:

The sum of the squares method in C# looks something like this:

public class SumOfSquares
{
  public static int CalculateSquaresSum(int n)
  {
    var sum = 0;
    for (var i = 1; i <= n; i++)
    {
      sum += Square(i);
    }
    return sum;
  }
  public static int Square(int x)
  {
    return x * x;
  }
}

Again, the C# version is quite verbose and can be made more functional by using LINQ as seen next:

public static int SquaresSum(int n)
{
  return Enumerable.Range(1, n)
  .Select(i => i * i)
  .Sum();
}

This can be further reduced to the following code:

public static int SquaresSum(int n)
{
  return Enumerable.Range(1, n)
  .Sum(i => i * i);
}

In this case, IEnumerable is used along with a Select filter, which sums up the results. Numbers from a sequence are each squared and aggregated into a sum.

Project Euler provides a series of mathematical and programming problems that can be solved using programming languages of your choice. Following is problem #1 from Project Euler:

An F# solution to this problem can be written as follows:

let total = [1..999] |> List.map (fun i -> if i % 5 = 0 || i % 3 = 0 then i else 0) |> List.sum

In this case we operate on 1-999, chain the operator with map to perform a modulus operation, and then sum up the results. An alternate approach is to use a filter that categorizes the results and provides a collection to perform a sum on. This approach can be listed as follows:

let total = [1..999] |> List.filter (fun i -> i % 5 = 0 || i % 3 = 0) |> List.sum

The solution in C# following the same algorithm results in a verbose listing as seen here:

public static int CalcSumOfMultiples()
{
  int result = 0;
  for (int i = 1; i < 1000; i++)
  {
    if ((i % 3) == 0 || (i % 5) == 0)
    {
      result += i;
    }
  }
  return result;
}

This C# code can be LINQ'ified to a more terse syntax as follows:

var total = Enumerable.Range(1, 999).Select(x => x % 3 == 0 || x % 5 == 0 ? x : 0).Sum();

Another better way of doing this can be seen in the next code listing:

var total = Enumerable.Range(1, 999).Sum(x => x%3 == 0 || x%5 == 0 ? x : 0);

The F# solutions of Project Euler problems, to further help understand algorithms and data structures can be found at https://github.com/adnanmasood/Euler.Polyglot.

And now on to the language wars!

A common inquiry among seasoned C# developers is, "What is the benefit of using F#? Or to word it differently, why do I need to learn a new language when I can perform the same tasks in the language I already know and love?"

A good analogy is LaTeX versus Microsoft Word. You may have used LaTeX for typesetting. For complicated tasks, Word becomes too complex or even unusable. Marko Pinteric explains why you would want to use LaTeX instead of Word with the following graph:

Complexity and learning curve. Using LaTeX on Windows by Marko Pinteric (www.pinteric.com/miktex.html)

The same applies to F#. Functional programming does have a learning curve but it equips you with the tools needed to go further in algorithmic software development. This eventually leads to the argument of general benefits of functional programming over imperative and object oriented languages.

Using functional programming with F#, one can arguably formulate and design solutions in an easier, more effective manner, especially if these problems pertain to the algorithmic domain. As a functional language, F# facilitates keeping the problem closer to their definition in a concise and terse manner. From the testability perspective, the resulting code becomes less error-prone due to its powerful type system, intuitive recursive representation of algorithms, and built-in immutability. Data structure immutability is especially helpful in the case of multi-threaded scenarios. This is, in essence, due to built-in data type immutability.

The specific F# advantages include the following:

Any functional language in general, and F# in particular, is not a silver bullet and shouldn't be treated as one. For UI centric and other applications of highly stateful nature, C# and other imperative .NET languages are a better fit than a functional programming language. Having said that, if you are a quant, who is writing high frequency trading algorithms in F#, or a rewriting to improve an existing VWAP implementation, you will be delighted to know that you can easily expose the F# functionality using your server-side C# WCF libraries. However, since you can have F# and C# together in one .NET solution, it is easy to combine the benefits of both languages and use as needed.

To summarize, F# provides the combined benefits of succinct syntax, immutable types, interoperability, efficiency, concurrency, and scalability— an impressive list. Functional programming has a well established repertoire as an efficient way of modeling complex problems in its respective mathematical form. F#, as a modern multi-paradigm language, is quite practical for enterprises, and gives developers and software architects an excellent reason to start using functional programming in their projects.

We recommend reading Functional thinking: Why functional programming is on the rise, by Neal Ford, who is a software architect at ThoughtWorks, at www.ibm.com/developerworks/library/j-ft20/ as a follow up reading to reinforce some of the concepts discussed in this chapter.

In this chapter, we have covered an introduction to functional programming paradigm along with some key syntactical elements of the F# programming language. We have established the notion of thinking in functional style and explained why functional programming matters? We also elaborated on the benefits of functional programming and functional data structures along with code based comparisons of imperative and functional paradigms.

In the next chapter, we will gain further knowledge about the F# tooling, syntax, and semantics of the language and learn to write some programs using F#.