Multiple linear regression
We've seen so far in this chapter how to build a regression line with one independent variable. However, it is often desirable to build a model with several independent variables. This is called multiple linear regression.
Each independent variable is going to need its own coefficient. Rather than working our way through the alphabet to represent each one, let's designate a new variable β, pronounced "beta", to hold all of our coefficients:

This model is equivalent to our bivariate linear regression model, where  and
and  so long as we ensure that x1 is always equal to one. This ensures that β1 is always a constant factor representing our intercept. x1 is called the bias term.
so long as we ensure that x1 is always equal to one. This ensures that β1 is always a constant factor representing our intercept. x1 is called the bias term.
Having generalized the linear equation in terms of beta, easy to extend to as many coefficients as we'd like:
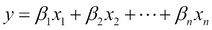
Each of the values of x1 up to xn correspond to an independent variable that might help explain the value of y. Each of the values of β1 up to βn correspond to a coefficient that determines...






















































