Baxter's arms
Baxter has seven rotary joints as shown in the following figure. Each arm is often referred to as a 7-DOF arm, since motion of the arm is controlled by seven actuators (motors) that are capable of independent rotation.
Baxter's 7-DOF arms are described on the Rethink Robotics site at http://sdk.rethinkrobotics.com/wiki/Arms.
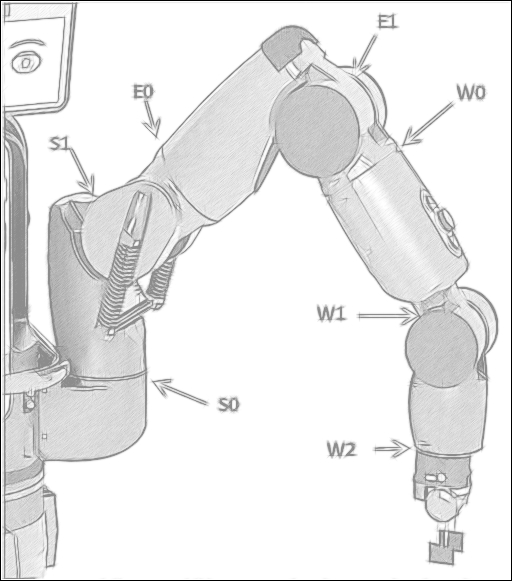
Baxter's arm joints
The arm joints are named in the following manner:
S0: Shoulder Roll
S1: Shoulder Pitch
E0: Elbow Roll
E1: Elbow Pitch
W0: Wrist Roll
W1: Wrist Pitch
W2: Wrist Roll
The designation of the joints as S0, S1, E0, E1, W0, W1, and W2 enables us to define and even monitor each of the angles for these joints with respect to the coordinates of the joints. The angles are measured in ROS in radians. As there are 2π radians in a complete circle, one radian is 360/(2π) or about 57.3 degrees. A 90-degree angle is π/4 or about 0.7854 radians. These conversion values are given because it is often required to move the joints to a 90-degree position or other angle...


























































