The accumulator idiom
These methods are easy to understand. However, for unbalanced trees, concatenating long lists could be slow, very slow.
We could eliminate list concatenation by sending the result list as an accumulator argument:
scala> def preorderAcc[A](tree: BinTree[A], acc: List[A]): List[A] = tree match {
| case Leaf => acc
| case Branch(v, l, r) => v :: preorderAcc(l, preorderAcc(r, acc))
| }
scala> println(preorderAcc(t, Nil))
List(1, 2, 5, 9)
The method now takes an additional argument: acc. We always set it to Nil when we call the method.
As in preorder, we have two cases.
The first clause is as follows:
case Leaf => acc
This just returns the already accumulated values, if any.
The second clause is as follows:
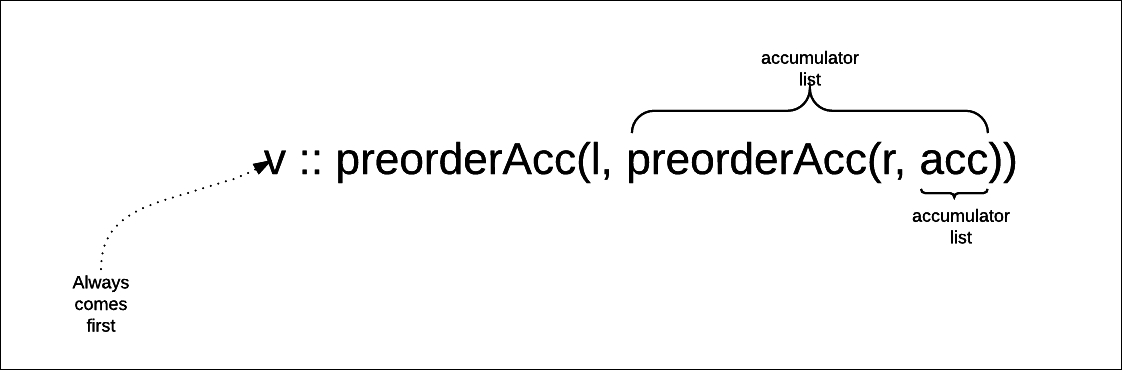
case Branch(v, l, r) => v :: preorderAcc(l, preorderAcc(r, acc))
This prepends the value v to the result of calling preorder on both the subtrees:
A nice way to trace out how the accumulator grows is to add a judicious print...


































































