Syntactical similarities and differences

Let's expand upon the preceding example and compare the syntactical differences between F# and C# through another simple example, the sum of a square method. A shorter and elegant looking functional syntax follows:

let square x = x * x
let sumOfSquares n = [1..n] |> List.map square |> List.sum 

Here you see the use of one of F#'s celebrated operators, that is, the |> pipe forward operator. It essentially performs piping operations by passing the results from left the side of the function to the right side, and can be concatenated.

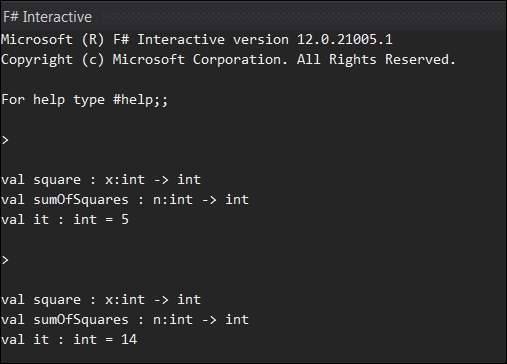
Running this program in F# the interactive console yields the following results for

sumOfSquares 2 

and

sumOfSquares 3 

respectively:

The sum of the squares method in C# looks something like this:

public class SumOfSquares
{
  public static int CalculateSquaresSum(int n)
  {
    var sum = 0;
    for (var i = 1; i <= n; i++)
    {
      sum += Square(i);
    }
    return sum;
  }
  public static int Square(int x)
  {
    return x * x;
  }
}

Again, the C# version is quite verbose and can be made more functional by using LINQ as seen next:

public static int SquaresSum(int n)
{
  return Enumerable.Range(1, n)
  .Select(i => i * i)
  .Sum();
}

This can be further reduced to the following code:

public static int SquaresSum(int n)
{
  return Enumerable.Range(1, n)
  .Sum(i => i * i);
}

In this case, IEnumerable is used along with a Select filter, which sums up the results. Numbers from a sequence are each squared and aggregated into a sum.

Project Euler provides a series of mathematical and programming problems that can be solved using programming languages of your choice. Following is problem #1 from Project Euler:

If we list all the natural numbers below 10 that are multiples of 3 or 5, we get 3, 5, 6 and 9. The sum of these multiples is 23 Find the sum of all the multiples of 3 or 5 below 1000.

An F# solution to this problem can be written as follows:

let total = [1..999] |> List.map (fun i -> if i % 5 = 0 || i % 3 = 0 then i else 0) |> List.sum

In this case we operate on 1-999, chain the operator with map to perform a modulus operation, and then sum up the results. An alternate approach is to use a filter that categorizes the results and provides a collection to perform a sum on. This approach can be listed as follows:

let total = [1..999] |> List.filter (fun i -> i % 5 = 0 || i % 3 = 0) |> List.sum

The solution in C# following the same algorithm results in a verbose listing as seen here:

public static int CalcSumOfMultiples()
{
  int result = 0;
  for (int i = 1; i < 1000; i++)
  {
    if ((i % 3) == 0 || (i % 5) == 0)
    {
      result += i;
    }
  }
  return result;
}

This C# code can be LINQ'ified to a more terse syntax as follows:

var total = Enumerable.Range(1, 999).Select(x => x % 3 == 0 || x % 5 == 0 ? x : 0).Sum();

Another better way of doing this can be seen in the next code listing:

var total = Enumerable.Range(1, 999).Sum(x => x%3 == 0 || x%5 == 0 ? x : 0);

The F# solutions of Project Euler problems, to further help understand algorithms and data structures can be found at https://github.com/adnanmasood/Euler.Polyglot.