Vectors and 2D coordinate systems
This section is a very brief overview of 2D coordinate systems and vector math as it’s used in game development. Vector math is an essential tool in game development, so if you need a broader understanding of the topic, see Khan Academy’s linear algebra series (https://www.khanacademy.org/math/linear-algebra).
When working in 2D, you’ll use Cartesian coordinates to identify locations in the 2D plane. A particular position in 2D space is written as a pair of values, such as (4, 3), representing the position along the x and y axes, respectively. Any position in the 2D plane can be described in this way.
In 2D space, Godot follows the common computer graphics practice of orienting the x axis to the right and the y axis downward:
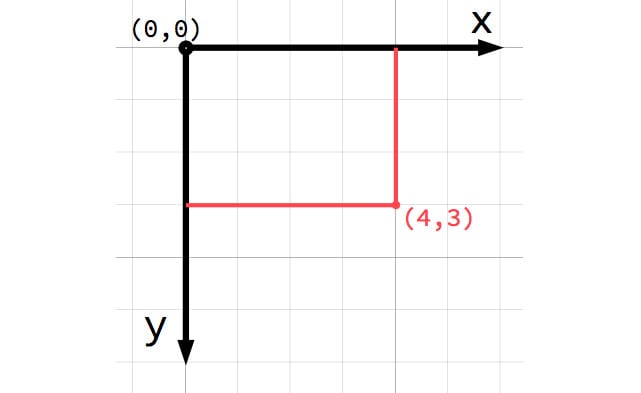
Figure 2.5: A 2D coordinate system
That’s not what my math teacher taught me!
If you’re new to computer graphics or game development, it might seem odd that the positive y axis points downward instead of upward, which you likely learned in math class. However, this orientation is very common in computer graphics applications.
Vectors
You can also think of the (4, 3) position as an offset from the (0, 0) point, or origin. Imagine an arrow pointing from the origin to the point:
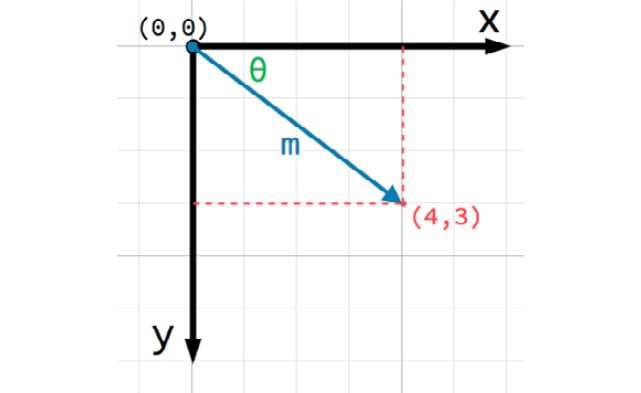
Figure 2.6: A 2D vector
This arrow is a vector. It represents a great deal of useful information, including the point’s location, its distance or length (m), and its angle from the x axis (θ). More specifically, this type of vector is referred to as a position vector – that is, one that describes a position in space. Vectors can also represent movement, acceleration, or any other quantity that has a size and a direction.
In Godot, vectors have a wide array of uses, and you’ll use them in every project in this book.
You should now have an understanding of how the 2D coordinate space works and how vectors can help to position and move objects. In the next section, you’ll create the player object and use this knowledge to control its movement.


























































