QR decomposition of a matrix
The general linear regression model calculation requires us to find the inverse of the matrix, which can be computationally expensive for bigger matrices. A decomposition scheme, such as QR and SVD, helps in that regard.
QR decomposition breaks a given matrix into two different matrices—Q and R, such that when these two are multiplied, the original matrix is found.
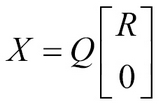
In the preceding image, X is an n x p matrix with n rows and p columns, R is an upper diagonal matrix, and Q is an n x n matrix given by:
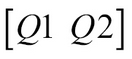
Here, Q1 is the first p columns of Q and Q2 is the last n – p columns of Q.
Using the Math.Net method QR you can find QR factorization:

Just to prove the fact that you will get the original matrix back, you can multiply Q and R to see if you get the original matrix back:
let myMatAgain = qr.Q * qr.R
SVD of a matrix
SVD stands for Single Value Decomposition. In this a matrix, X is represented by three matrices (the definition of SVD is taken from Wikipedia...































































