Decision tree learning

Decision tree classifiers are attractive models if we care about interpretability. As the name “decision tree” suggests, we can think of this model as breaking down our data by making a decision based on asking a series of questions.

Let’s consider the following example in which we use a decision tree to decide upon an activity on a particular day:

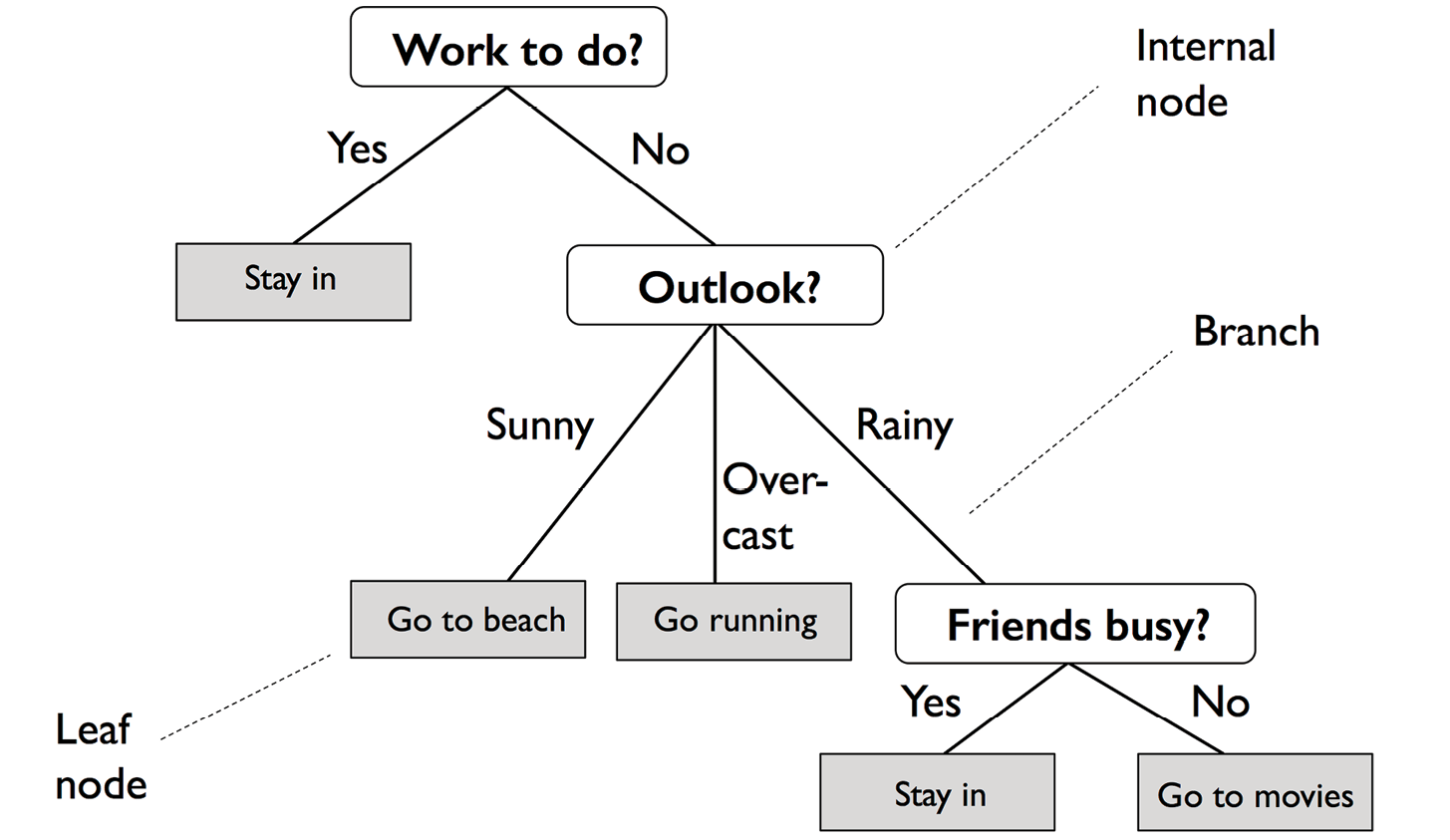
Figure 3.18: An example of a decision tree

Based on the features in our training dataset, the decision tree model learns a series of questions to infer the class labels of the examples. Although Figure 3.18 illustrates the concept of a decision tree based on categorical variables, the same concept applies if our features are real numbers, like in the Iris dataset. For example, we could simply define a cut-off value along the sepal width feature axis and ask a binary question: “Is the sepal width ≥ 2.8 cm?”

Using the decision algorithm, we start at the tree root and split the data on the feature that results in the largest information gain (IG), which will be explained in more detail in the following section. In an iterative process, we can then repeat this splitting procedure at each child node until the leaves are pure. This means that the training examples at each node all belong to the same class. In practice, this can result in a very deep tree with many nodes, which can easily lead to overfitting. Thus, we typically want to prune the tree by setting a limit for the maximum depth of the tree.

Maximizing IG – getting the most bang for your buck

To split the nodes at the most informative features, we need to define an objective function to optimize via the tree learning algorithm. Here, our objective function is to maximize the IG at each split, which we define as follows:

Here, f is the feature to perform the split; D_p and D_j are the dataset of the parent and jth child node; I is our impurity measure; N_p is the total number of training examples at the parent node; and N_j is the number of examples in the jth child node. As we can see, the information gain is simply the difference between the impurity of the parent node and the sum of the child node impurities—the lower the impurities of the child nodes, the larger the information gain. However, for simplicity and to reduce the combinatorial search space, most libraries (including scikit-learn) implement binary decision trees. This means that each parent node is split into two child nodes, D_left and D_right:

The three impurity measures or splitting criteria that are commonly used in binary decision trees are Gini impurity (I_G), entropy (I_H), and the classification error (I_E). Let’s start with the definition of entropy for all non-empty classes ():

Here, p(i|t) is the proportion of the examples that belong to class i for a particular node, t. The entropy is therefore 0 if all examples at a node belong to the same class, and the entropy is maximal if we have a uniform class distribution. For example, in a binary class setting, the entropy is 0 if p(i=1|t) = 1 or p(i=0|t) = 0. If the classes are distributed uniformly with p(i=1|t) = 0.5 and p(i=0|t) = 0.5, the entropy is 1. Therefore, we can say that the entropy criterion attempts to maximize the mutual information in the tree.

To provide a visual intuition, let us visualize the entropy values for different class distributions via the following code:

>>> def entropy(p):
...     return - p * np.log2(p) - (1 - p) * np.log2((1 - p))
>>> x = np.arange(0.0, 1.0, 0.01)
>>> ent = [entropy(p) if p != 0 else None for p in x]
>>> plt.ylabel('Entropy')
>>> plt.xlabel('Class-membership probability p(i=1)')
>>> plt.plot(x, ent)
>>> plt.show()

Figure 3.19 below shows the plot produced by the preceding code:

Figure 3.19: Entropy values for different class-membership probabilities

The Gini impurity can be understood as a criterion to minimize the probability of misclassification:

Similar to entropy, the Gini impurity is maximal if the classes are perfectly mixed, for example, in a binary class setting (c = 2):

However, in practice, both the Gini impurity and entropy typically yield very similar results, and it is often not worth spending much time on evaluating trees using different impurity criteria rather than experimenting with different pruning cut-offs. In fact, as you will see later in Figure 3.21, both the Gini impurity and entropy have a similar shape.

Another impurity measure is the classification error:

This is a useful criterion for pruning, but not recommended for growing a decision tree, since it is less sensitive to changes in the class probabilities of the nodes. We can illustrate this by looking at the two possible splitting scenarios shown in Figure 3.20:

Figure 3.20: Decision tree data splits

We start with a dataset, D_p, at the parent node, which consists of 40 examples from class 1 and 40 examples from class 2 that we split into two datasets, D_left and D_right. The information gain using the classification error as a splitting criterion would be the same (IG_E = 0.25) in both scenarios, A and B:

However, the Gini impurity would favor the split in scenario B () over scenario A (IG_G = 0.125), which is indeed purer:

Similarly, the entropy criterion would also favor scenario B (IG_H = 0.31) over scenario A (IG_H = 0.19):

For a more visual comparison of the three different impurity criteria that we discussed previously, let’s plot the impurity indices for the probability range [0, 1] for class 1. Note that we will also add a scaled version of the entropy (entropy / 2) to observe that the Gini impurity is an intermediate measure between entropy and the classification error. The code is as follows:

>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> def gini(p):
...     return p*(1 - p) + (1 - p)*(1 - (1-p))
>>> def entropy(p):
...     return - p*np.log2(p) - (1 - p)*np.log2((1 - p))
>>> def error(p):
...     return 1 - np.max([p, 1 - p])
>>> x = np.arange(0.0, 1.0, 0.01)
>>> ent = [entropy(p) if p != 0 else None for p in x]
>>> sc_ent = [e*0.5 if e else None for e in ent]
>>> err = [error(i) for i in x]
>>> fig = plt.figure()
>>> ax = plt.subplot(111)
>>> for i, lab, ls, c, in zip([ent, sc_ent, gini(x), err],
...                           ['Entropy', 'Entropy (scaled)',
...                            'Gini impurity',
...                            'Misclassification error'],
...                           ['-', '-', '--', '-.'],
...                           ['black', 'lightgray',
...                            'red', 'green', 'cyan']):
...     line = ax.plot(x, i, label=lab,
...                   linestyle=ls, lw=2, color=c)
>>> ax.legend(loc='upper center', bbox_to_anchor=(0.5, 1.15),
...           ncol=5, fancybox=True, shadow=False)
>>> ax.axhline(y=0.5, linewidth=1, color='k', linestyle='--')
>>> ax.axhline(y=1.0, linewidth=1, color='k', linestyle='--')
>>> plt.ylim([0, 1.1])
>>> plt.xlabel('p(i=1)')
>>> plt.ylabel('impurity index')
>>> plt.show()

The plot produced by the preceding code example is as follows:

Figure 3.21: The different impurity indices for different class-membership probabilities between 0 and 1

Building a decision tree

Decision trees can build complex decision boundaries by dividing the feature space into rectangles. However, we have to be careful since the deeper the decision tree, the more complex the decision boundary becomes, which can easily result in overfitting. Using scikit-learn, we will now train a decision tree with a maximum depth of 4, using the Gini impurity as a criterion for impurity.

Although feature scaling may be desired for visualization purposes, note that feature scaling is not a requirement for decision tree algorithms. The code is as follows:

>>> from sklearn.tree import DecisionTreeClassifier
>>> tree_model = DecisionTreeClassifier(criterion='gini',
...                                     max_depth=4,
...                                     random_state=1)
>>> tree_model.fit(X_train, y_train)
>>> X_combined = np.vstack((X_train, X_test))
>>> y_combined = np.hstack((y_train, y_test))
>>> plot_decision_regions(X_combined,
...                       y_combined,
...                       classifier=tree_model,
...                       test_idx=range(105, 150))
>>> plt.xlabel('Petal length [cm]')
>>> plt.ylabel('Petal width [cm]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()

After executing the code example, we get the typical axis-parallel decision boundaries of the decision tree:

Figure 3.22: The decision boundaries of the Iris data using a decision tree

A nice feature in scikit-learn is that it allows us to readily visualize the decision tree model after training via the following code:

>>> from sklearn import tree
>>> feature_names = ['Sepal length', 'Sepal width',
...                  'Petal length', 'Petal width']
>>> tree.plot_tree(tree_model,
...                feature_names=feature_names,
...                filled=True)
>>> plt.show()

Figure 3.23: A decision tree model fit to the Iris dataset

Setting filled=True in the plot_tree function we called colors the nodes by the majority class label at that node. There are many additional options available, which you can find in the documentation at https://scikit-learn.org/stable/modules/generated/sklearn.tree.plot_tree.html.

Looking at the decision tree figure, we can now nicely trace back the splits that the decision tree determined from our training dataset. Regarding the feature splitting criterion at each node, note that the branches to the left correspond to “True” and branches to the right correspond to “False.”

Looking at the root node, it starts with 105 examples at the top. The first split uses a sepal width cut-off ≤ 0.75 cm for splitting the root node into two child nodes with 35 examples (left child node) and 70 examples (right child node). After the first split, we can see that the left child node is already pure and only contains examples from the Iris-setosa class (Gini impurity = 0). The further splits on the right are then used to separate the examples from the Iris-versicolor and Iris-virginica class.

Looking at this tree, and the decision region plot of the tree, we can see that the decision tree does a very good job of separating the flower classes. Unfortunately, scikit-learn currently does not implement functionality to manually post-prune a decision tree. However, we could go back to our previous code example, change the max_depth of our decision tree to 3, and compare it to our current model, but we leave this as an exercise for the interested reader.

Alternatively, scikit-learn provides an automatic cost complexity post-pruning procedure for decision trees. Interested readers can find more information about this more advanced topic in the following tutorial: https://scikit-learn.org/stable/auto_examples/tree/plot_cost_complexity_pruning.html.

Combining multiple decision trees via random forests

Ensemble methods have gained huge popularity in applications of machine learning during the last decade due to their good classification performance and robustness toward overfitting. While we are going to cover different ensemble methods, including bagging and boosting, later in Chapter 7, Combining Different Models for Ensemble Learning, let’s discuss the decision tree-based random forest algorithm, which is known for its good scalability and ease of use. A random forest can be considered as an ensemble of decision trees. The idea behind a random forest is to average multiple (deep) decision trees that individually suffer from high variance to build a more robust model that has a better generalization performance and is less susceptible to overfitting. The random forest algorithm can be summarized in four simple steps:

1. Draw a random bootstrap sample of size n (randomly choose n examples from the training dataset with replacement).
2. Grow a decision tree from the bootstrap sample. At each node:
   1. Randomly select d features without replacement.
   2. Split the node using the feature that provides the best split according to the objective function, for instance, maximizing the information gain.
3. Repeat steps 1-2 k times.
4. Aggregate the prediction by each tree to assign the class label by majority vote. Majority voting will be discussed in more detail in Chapter 7.

We should note one slight modification in step 2 when we are training the individual decision trees: instead of evaluating all features to determine the best split at each node, we only consider a random subset of those.

Sampling with and without replacement

In case you are not familiar with the terms sampling “with” and “without” replacement, let’s walk through a simple thought experiment. Let’s assume that we are playing a lottery game where we randomly draw numbers from an urn. We start with an urn that holds five unique numbers, 0, 1, 2, 3, and 4, and we draw exactly one number on each turn. In the first round, the chance of drawing a particular number from the urn would be 1/5. Now, in sampling without replacement, we do not put the number back into the urn after each turn. Consequently, the probability of drawing a particular number from the set of remaining numbers in the next round depends on the previous round. For example, if we have a remaining set of numbers 0, 1, 2, and 4, the chance of drawing number 0 would become 1/4 in the next turn.

However, in random sampling with replacement, we always return the drawn number to the urn so that the probability of drawing a particular number at each turn does not change; we can draw the same number more than once. In other words, in sampling with replacement, the samples (numbers) are independent and have a covariance of zero. For example, the results from five rounds of drawing random numbers could look like this:

• Random sampling without replacement: 2, 1, 3, 4, 0
• Random sampling with replacement: 1, 3, 3, 4, 1

Although random forests don’t offer the same level of interpretability as decision trees, a big advantage of random forests is that we don’t have to worry so much about choosing good hyperparameter values. We typically don’t need to prune the random forest since the ensemble model is quite robust to noise from averaging the predictions among the individual decision trees. The only parameter that we need to care about in practice is the number of trees, k, (step 3) that we choose for the random forest. Typically, the larger the number of trees, the better the performance of the random forest classifier at the expense of an increased computational cost.

Although it is less common in practice, other hyperparameters of the random forest classifier that can be optimized—using techniques that we will discuss in Chapter 6, Learning Best Practices for Model Evaluation and Hyperparameter Tuning—are the size, n, of the bootstrap sample (step 1) and the number of features, d, that are randomly chosen for each split (step 2a), respectively. Via the sample size, n, of the bootstrap sample, we control the bias-variance tradeoff of the random forest.

Decreasing the size of the bootstrap sample increases the diversity among the individual trees since the probability that a particular training example is included in the bootstrap sample is lower. Thus, shrinking the size of the bootstrap samples may increase the randomness of the random forest, and it can help to reduce the effect of overfitting. However, smaller bootstrap samples typically result in a lower overall performance of the random forest and a small gap between training and test performance, but a low test performance overall. Conversely, increasing the size of the bootstrap sample may increase the degree of overfitting. Because the bootstrap samples, and consequently the individual decision trees, become more similar to one another, they learn to fit the original training dataset more closely.

In most implementations, including the RandomForestClassifier implementation in scikit-learn, the size of the bootstrap sample is chosen to be equal to the number of training examples in the original training dataset, which usually provides a good bias-variance tradeoff. For the number of features, d, at each split, we want to choose a value that is smaller than the total number of features in the training dataset. A reasonable default that is used in scikit-learn and other implementations is , where m is the number of features in the training dataset.

Conveniently, we don’t have to construct the random forest classifier from individual decision trees by ourselves because there is already an implementation in scikit-learn that we can use:

>>> from sklearn.ensemble import RandomForestClassifier
>>> forest = RandomForestClassifier(n_estimators=25,
...                                 random_state=1,
...                                 n_jobs=2)
>>> forest.fit(X_train, y_train)
>>> plot_decision_regions(X_combined, y_combined,
...                       classifier=forest, test_idx=range(105,150))
>>> plt.xlabel('Petal length [cm]')
>>> plt.ylabel('Petal width [cm]')
>>> plt.legend(loc='upper left')
>>> plt.tight_layout()
>>> plt.show()

After executing the preceding code, we should see the decision regions formed by the ensemble of trees in the random forest, as shown in Figure 3.24:

Figure 3.24: Decision boundaries on the Iris dataset using a random forest

Using the preceding code, we trained a random forest from 25 decision trees via the n_estimators parameter. By default, it uses the Gini impurity measure as a criterion to split the nodes. Although we are growing a very small random forest from a very small training dataset, we used the n_jobs parameter for demonstration purposes, which allows us to parallelize the model training using multiple cores of our computer (here, two cores). If you encounter errors with this code, your computer may not support multiprocessing. You can omit the n_jobs parameter or set it to n_jobs=None.