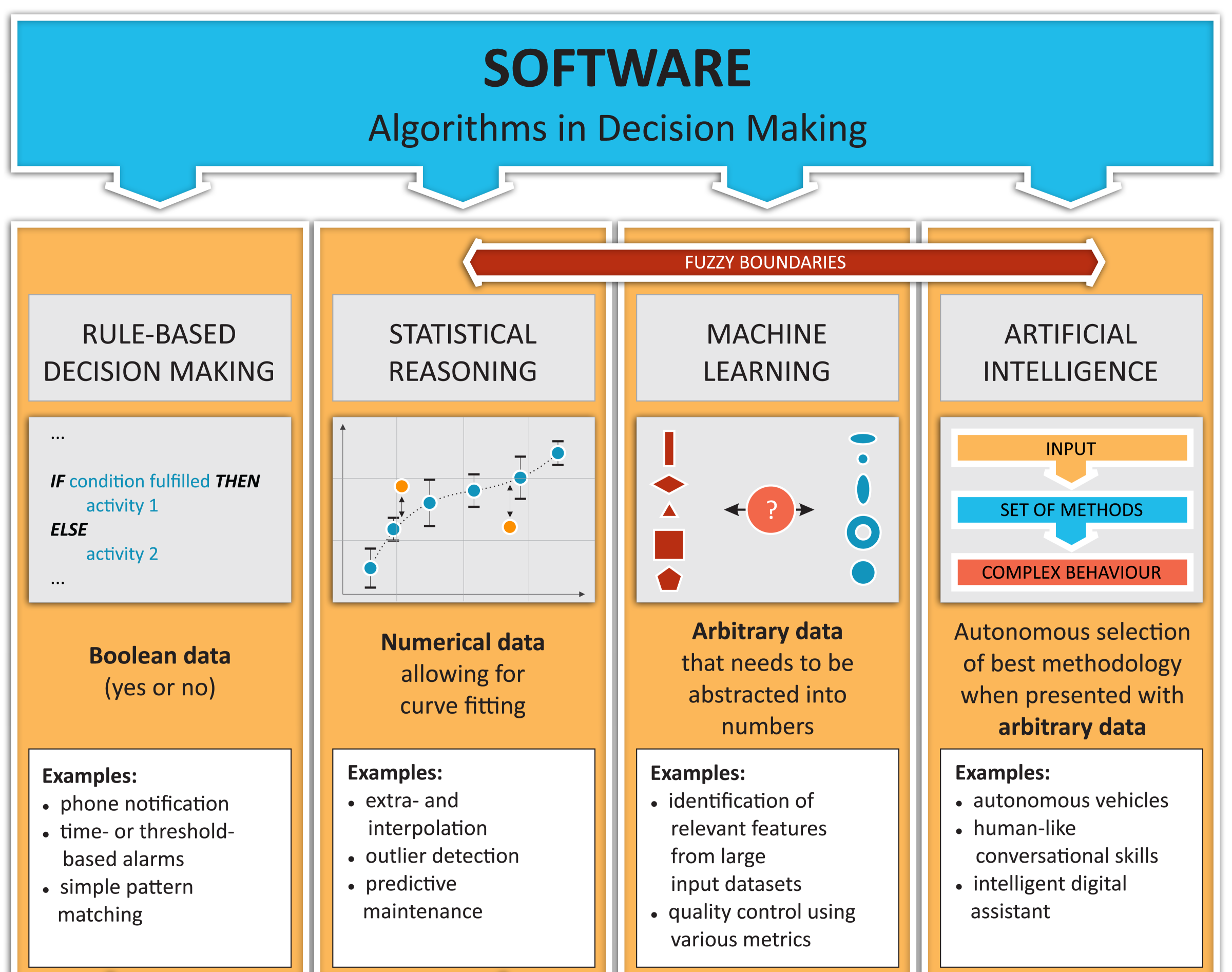
Machine learning as a discipline is not an isolated field—it is framed inside a wider domain, Artificial Intelligence (AI). But as you can guess, machine learning didn't appear from the void. As a discipline it has its predecessors, and it has been evolving in stages of increasing complexity in the following four clearly differentiated steps:
- The first model of machine learning involved rule-based decisions and a simple level of data-based algorithms that includes in itself, and as a prerequisite, all the possible ramifications and decision rules, implying that all the possible options will be hardcoded into the model beforehand by an expert in the field. This structure was implemented in the majority of applications developed since the first programming languages appeared in 1950. The main data type and function being handled by this kind of algorithm is the Boolean, as it exclusively dealt with yes or no decisions.
- During the second developmental stage of statistical reasoning, we started to let the probabilistic characteristics of the data have a say, in addition to the previous choices set up in advance. This better reflects the fuzzy nature of real-world problems, where outliers are common and where it is more important to take into account the nondeterministic tendencies of the data than the rigid approach of fixed questions. This discipline adds to the mix of mathematical tools elements of Bayesian probability theory. Methods pertaining to this category include curve fitting (usually of linear or polynomial), which has the common property of working with numerical data.
- The machine learning stage is the realm in which we are going to be working throughout this book, and it involves more complex tasks than the simplest Bayesian elements of the previous stage.
The most outstanding feature of machine learning algorithms is that they can generalize models from data but the models are capable of generating their own feature selectors, which aren't limited by a rigid target function, as they are generated and defined as the training process evolves. Another differentiator of this kind of model is that they can take a large variety of data types as input, such as speech, images, video, text, and other data susceptible to being represented as vectors. - AI is the last step in the scale of abstraction capabilities that, in a way, include all previous algorithm types, but with one key difference: AI algorithms are able to apply the learned knowledge to solve tasks that had never been considered during training. The types of data with which this algorithm works are even more generic than the types of data supported by machine learning, and they should be able, by definition, to transfer problem-solving capabilities from one data type to another, without a complete retraining of the model. In this way, we could develop an algorithm for object detection in black and white images and the model could abstract the knowledge to apply the model to color images.
In the following diagram, we represent these four stages of development towards real AI applications: