Operations on tensors
We have seen how to create a computation graph composed of symbolic variables and operations, and compile the resulting expression for an evaluation or as a function, either on GPU or on CPU.
As tensors are very important to deep learning, Theano provides lots of operators to work with tensors. Most operators that exist in scientific computing libraries such as NumPy for numerical arrays have their equivalent in Theano and have a similar name, in order to be more familiar to NumPy's users. But contrary to NumPy, expressions written with Theano can be compiled either on CPU or GPU.
This, for example, is the case for tensor creation:
T.zeros(),T.ones(),T.eye()operators take a shape tuple as inputT.zeros_like(),T.one_like(),T.identity_like()use the shape of the tensor argumentT.arange(),T.mgrid(),T.ogrid()are used for range and mesh grid arrays
Let's have a look in the Python shell:
>>> a = T.zeros((2,3))
>>> a.eval()
array([[ 0., 0., 0.],
[ 0., 0., 0.]])
>>> b = T.identity_like(a)
>>> b.eval()
array([[ 1., 0., 0.],
[ 0., 1., 0.]])
>>> c = T.arange(10)
>>> c.eval()
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])Information such as the number of dimensions, ndim, and the type, dtype, are defined at tensor creation and cannot be modified later:
>>> c.ndim
1
>>> c.dtype
'int64'
>>> c.type
TensorType(int64, vector)Some other information, such as shape, is evaluated by the computation graph:
>>> a = T.matrix()
>>> a.shape
Shape.0
>>> a.shape.eval({a: [[1, 2], [1, 3]]})
array([2, 2])
>>> shape_fct = theano.function([a],a.shape)
>>> shape_fct([[1, 2], [1, 3]])
array([2, 2])
>>> n = T.iscalar()
>>> c = T.arange(n)
>>> c.shape.eval({n:10})
array([10])Dimension manipulation operators
The first type of operator on tensor is for dimension manipulation. This type of operator takes a tensor as input and returns a new tensor:
|
Operator |
Description |
|---|---|
|
|
Reshape the dimension of the tensor |
|
|
Fill the array with the same value |
|
|
Return all elements in a 1-dimensional tensor (vector) |
|
|
Change the order of the dimension, more or less like NumPy's transpose method – the main difference is that it can be used to add or remove broadcastable dimensions (of length 1). |
|
|
Reshape by removing dimensions equal to 1 |
|
|
Transpose |
|
|
Swap dimensions |
|
|
Sort tensor, or indices of the order |
For example, the reshape operation's output represents a new tensor, containing the same elements in the same order but in a different shape:
>>> a = T.arange(10)
>>> b = T.reshape( a, (5,2) )
>>> b.eval()
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])The operators can be chained:
>>> T.arange(10).reshape((5,2))[::-1].T.eval()
array([[8, 6, 4, 2, 0],
[9, 7, 5, 3, 1]])Notice the use of traditional [::-1] array access by indices in Python and the .T for T.transpose.
Elementwise operators
The second type of operations on multi-dimensional arrays is elementwise operators.
The first category of elementwise operations takes two input tensors of the same dimensions and applies a function, f, elementwise, which means on all pairs of elements with the same coordinates in the respective tensors f([a,b],[c,d]) = [ f(a,c), f(b,d)]. For example, here's multiplication:
>>> a, b = T.matrices('a', 'b')
>>> z = a * b
>>> z.eval({a:numpy.ones((2,2)).astype(theano.config.floatX), b:numpy.diag((3,3)).astype(theano.config.floatX)})
array([[ 3., 0.],
[ 0., 3.]])The same multiplication can be written as follows:
>>> z = T.mul(a, b)
T.add and T.mul accept an arbitrary number of inputs:
>>> z = T.mul(a, b, a, b)
Some elementwise operators accept only one input tensor f([a,b]) = [f(a),f(b)]):
>>> a = T.matrix()
>>> z = a ** 2
>>> z.eval({a:numpy.diag((3,3)).astype(theano.config.floatX)})
array([[ 9., 0.],
[ 0., 9.]])Lastly, I would like to introduce the mechanism of broadcasting. When the input tensors do not have the same number of dimensions, the missing dimension will be broadcasted, meaning the tensor will be repeated along that dimension to match the dimension of the other tensor. For example, taking one multi-dimensional tensor and a scalar (0-dimensional) tensor, the scalar will be repeated in an array of the same shape as the multi-dimensional tensor so that the final shapes will match and the elementwise operation will be applied, f([a,b], c) = [ f(a,c), f(b,c) ]:
>>> a = T.matrix()
>>> b = T.scalar()
>>> z = a * b
>>> z.eval({a:numpy.diag((3,3)).astype(theano.config.floatX),b:3})
array([[ 6., 0.],
[ 0., 6.]])Here is a list of elementwise operations:
|
Operator |
Other form |
Description |
|---|---|---|
|
|
|
Add, subtract, multiply, divide |
|
|
|
Power, square root |
|
|
Exponential, logarithm | |
|
|
Cosine, sine, tangent | |
|
|
Hyperbolic trigonometric functions | |
|
|
|
Int div, modulus |
|
|
Rounding operators | |
|
|
Sign | |
|
|
|
Bitwise operators |
|
|
|
Comparison operators |
|
|
Equality, inequality, or close with tolerance | |
|
|
Comparison with NaN (not a number) | |
|
|
Absolute value | |
|
|
Minimum and maximum elementwise | |
|
|
Clip the values between a maximum and a minimum | |
|
|
Switch | |
|
|
Tensor type casting |
The elementwise operators always return an array with the same size as the input array. T.switch and T.clip accept three inputs.
In particular, T.switch will perform the traditional switch operator elementwise:
>>> cond = T.vector('cond')
>>> x,y = T.vectors('x','y')
>>> z = T.switch(cond, x, y)
>>> z.eval({ cond:[1,0], x:[10,10], y:[3,2] })
array([ 10., 2.], dtype=float32)At the same position where cond tensor is true, the result has the x value; otherwise, if it is false, it has the y value.
For the T.switch operator, there is a specific equivalent, ifelse, that takes a scalar condition instead of a tensor condition. It is not an elementwise operation though, and supports lazy evaluation (not all elements are computed if the answer is known before it finishes):
>>> from theano.ifelse import ifelse >>> z=ifelse(1, 5, 4) >>> z.eval() array(5, dtype=int8)
Reduction operators
Another type of operation on tensors is reductions, reducing all elements to a scalar value in most cases, and for that purpose, it is required to scan all the elements of the tensor to compute the output:
|
Operator |
Description |
|---|---|
|
|
Maximum, index of the maximum |
|
|
Minimum, index of the minimum |
|
|
Sum or product of elements |
|
|
Mean, variance, and standard deviation |
|
|
AND and OR operations with all elements |
|
|
Range of elements (minimum, maximum) |
These operations are also available row-wise or column-wise by specifying an axis and the dimension along which the reduction is performed:
>>> a = T.matrix('a')
>>> T.max(a).eval({a:[[1,2],[3,4]]})
array(4.0, dtype=float32)
>>> T.max(a,axis=0).eval({a:[[1,2],[3,4]]})
array([ 3., 4.], dtype=float32)
>>> T.max(a,axis=1).eval({a:[[1,2],[3,4]]})
array([ 2., 4.], dtype=float32)Linear algebra operators
A third category of operations are the linear algebra operators, such as matrix multiplication:
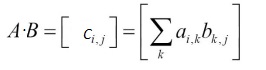
Also called inner product for vectors:
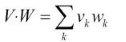
|
Operator |
Description |
|---|---|
|
|
Matrix multiplication/inner product |
|
|
Outer product |
There are some generalized (T.tensordot to specify the axis), or batched (batched_dot, batched_tensordot) versions of the operators.
Lastly, a few operators remain and can be very useful, but they do not belong to any of the previous categories: T.concatenate concatenates the tensors along the specified dimension, T.stack creates a new dimension to stack the input tensors, and T.stacklist creates new patterns to stack tensors together:
>>> a = T.arange(10).reshape((5,2))
>>> b = a[::-1]
>>> b.eval()
array([[8, 9],
[6, 7],
[4, 5],
[2, 3],
[0, 1]])
>>> a.eval()
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
>>> T.concatenate([a,b]).eval()
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9],
[8, 9],
[6, 7],
[4, 5],
[2, 3],
[0, 1]])
>>> T.concatenate([a,b],axis=1).eval()
array([[0, 1, 8, 9],
[2, 3, 6, 7],
[4, 5, 4, 5],
[6, 7, 2, 3],
[8, 9, 0, 1]])
>>> T.stack([a,b]).eval()
array([[[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]],
[[8, 9],
[6, 7],
[4, 5],
[2, 3],
[0, 1]]])An equivalent of the NumPy expressions a[5:] = 5 and a[5:] += 5 exists as two functions:
>>> a.eval()
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
>>> T.set_subtensor(a[3:], [-1,-1]).eval()
array([[ 0, 1],
[ 2, 3],
[ 4, 5],
[-1, -1],
[-1, -1]])
>>> T.inc_subtensor(a[3:], [-1,-1]).eval()
array([[0, 1],
[2, 3],
[4, 5],
[5, 6],
[7, 8]])Unlike NumPy's syntax, the original tensor is not modified; instead, a new variable is created that represents the result of that modification. Therefore, the original variable a still refers to the original value, and the returned variable (here unassigned) represents the updated one, and the user should use that new variable in the rest of their computation.













































































