5.8 Unitary transformations
What are the characteristics of linear transformations that preserve length? If L: V → V and it is always true that ‖L(v)‖ = ‖v‖, what can we say about the matrix of L?
A complex square matrix U is unitary if its adjoint U † is its inverse U –1. Hence, U U † = U † U = I. The columns of U are orthonormal, as are the rows, which follows from the definition of the complex inner product. matrix$unitary unitary$matrix
For a unitary matrix U, |det(U)| = 1 because

To prove that unitary matrices preserve length, we must do more transposition and conjugation math:
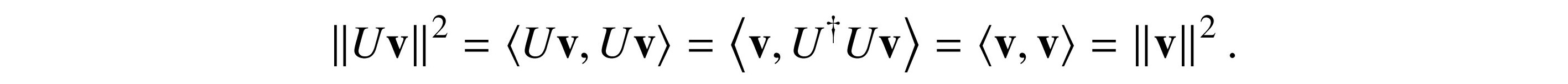
Since the lengths are nonnegative, ‖U v‖ = ‖v‖. Conversely, if this holds, we must have U† U = I.
Rotations and reflections are unitary. An orthogonal matrix is unitary.
...
































































