Matrices are two-dimensional arrays, categorized by rows and columns. They are important in graphics manipulation and AI; namely, image recognition. Matrices are commonly used for graphics since the rows and columns that reside within a matrix can correspond to the row and column arrangement of pixels on a screen, as well as because we can have the matrix values correspond to a particular color. Matrices are also frequently used for digital sound processing as digital audio signals are filtered and compressed using Fourier transforms, and matrices help with performing these actions.
Matrices are usually denoted with an M × N naming scheme, where M is the number of rows in the matrix and N is the number of columns in the matrix, as shown in the following image:
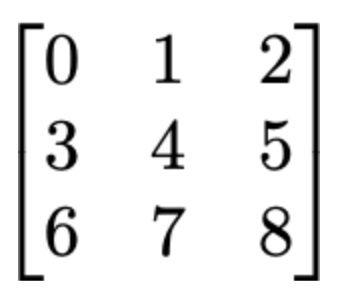
The preceding image, for example, is a 3 x 3 matrix. An M x N matrix is one of the core tenants...








































































