6.6 Expectation
Let’s look at the numeric finite discrete distribution of the random variable X with the probabilities given in this table: expected value expectation

If the process producing these values continues over time, what value would we “expect” to see?
If they all have the same probability of occurring, the expected value or expectation, E(X) is their average:

Note that the answer does not need to be, and often isn’t, one of the values in the distribution.
Since each value of X has a given probability, the expected value is instead the weighted average
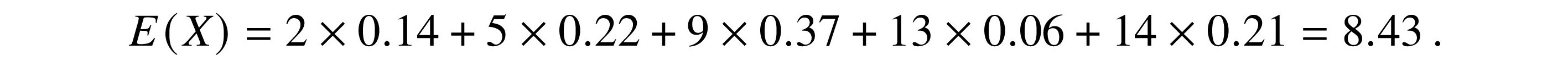
If someone simply gives you a list of values for a random variable, you can assume a uniform distribution, and the expected value is the usual average or mean. We sometimes use the notation μ(X) instead of E(X). μ is the lowercase Greek letter “mu.” μ`italic
If X is a random...
































































