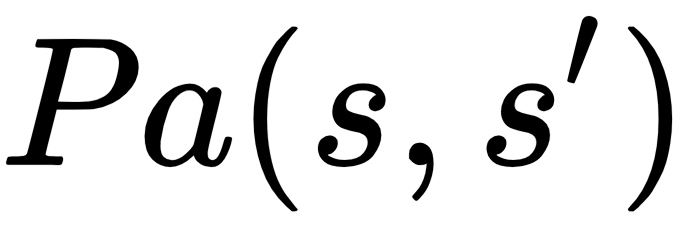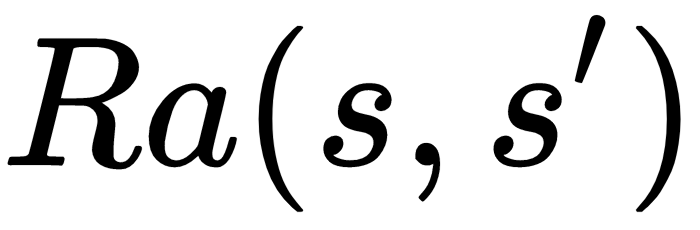In the previous step 1, the agent went from F or state 1 or s to B, which was state 2 or s'.
To do that, there was a strategy—a policy represented by P. All of this can be shown in one mathematical expression, the MDP state transition function:
P is the policy, the strategy made by the agent to go from F to B through action a. When going from F to B, this state transition is called state transition function:
- a is the action
- s is state 1 (F) and s' is state 2 (B)
This is the basis of MDP. The reward (right or wrong) is represented in the same way:
That means R is the reward for the action of going from state s to state s'. Going from one state to another will be a random process. This means that potentially, all states can go to another state.
The example we will be working on inputs a reward matrix so that the program can choose its best course of action. Then, the agent will go from state to state, learning the best trajectories for every possible starting location point. The goal of the MDP is to go to C (line 3, column 3 in the reward matrix), which has a starting value of 100 in the following Python code.
# Markov Decision Process (MDP) - The Bellman equations adapted to
# Reinforcement Learning
# R is The Reward Matrix for each state
R = ql.matrix([ [0,0,0,0,1,0],
[0,0,0,1,0,1],
[0,0,100,1,0,0],
[0,1,1,0,1,0],
[1,0,0,1,0,0],
[0,1,0,0,0,0] ])
Each line in the matrix in the example represents a letter from A to F, and each column represents a letter from A to F. All possible states are represented. The 1 values represent the nodes (vertices) of the graph. Those are the possible locations. For example, line 1 represents the possible moves for letter A, line 2 for letter B, and line 6 for letter F. On the first line, A cannot go to C directly, so a 0 value is entered. But, it can go to E, so a 1 value is added.
Some models start with -1 for impossible choices, such as B going directly to C and 0 values to define the locations. This model starts with 0 and 1 values. It sometimes takes weeks to design functions that will create a reward matrix (see Chapter 2, Think like a Machine).
There are several properties of this decision process. A few of them are mentioned here:
- The Markov property: The process is applied when the past is not taken into account. It is the memoryless property of this decision process, just as you do in a car with a guiding system. You move forward to reach your goal. This is called the Markov property.
- Unsupervised learning: From this memoryless Markov property, it is safe to say that the MDP is not supervised learning. Supervised learning would mean that we would have all the labels of the trip. We would know exactly what A means and use that property to make a decision. We would be in the future looking at the past. MDP does not take these labels into account. This means that this is unsupervised learning. A decision has to be made in each state without knowing the past states or what they signify. It means that the car, for example, was on its own at each location, which is represented by each of its states.
- Stochastic process: In step 1, when state B was reached, the agent controlling the mapping system and the driver didn't agree on where to go. A random choice could be made in a trial-and-error way, just like a coin toss. It is going to be a heads-or-tails process. The agent will toss the coin thousands of times and measure the outcomes. That's precisely how MDP works and how the agent will learn.
- Reinforcement learning: Repeating a trial and error process with feedback from the agent's environment.
- Markov chain: The process of going from state to state with no history in a random, stochastic way is called a Markov chain.
To sum it up, we have three tools:
- Pa(s,s'): A policy, P, or strategy to move from one state to another
- Ta(s,s'): A T, or stochastic (random) transition, function to carry out that action
- Ra(s,s'): An R, or reward, for that action, which can be negative, null, or positive
T is the transition function, which makes the agent decide to go from one point to another with a policy. In this case, it will be random. That's what machine power is for, and that's how reinforcement learning is often implemented.
Randomness is a property of MDP.
The following code describes the choice the agent is going to make.
next_action = int(ql.random.choice(PossibleAction,1))
return next_action
Once the code has been run, a new random action (state) has been chosen.
The Bellman equation is the road to programming reinforcement learning.
Bellman's equation completes the MDP. To calculate the value of a state, let's use Q, for the Q action-reward (or value) function. The pre-source code of Bellman's equation can be expressed as follows for one individual state:
The source code then translates the equation into a machine representation as in the following code:
# The Bellman equation
Q[current_state, action] = R[current_state, action] + gamma * MaxValue
The source code variables of the Bellman equation are as follows:
- Q(s): This is the value calculated for this state—the total reward. In step 1 when the agent went from F to B, the driver had to be happy. Maybe she/he had a crunch in a candy bar to feel good, which is the human counterpart of the reward matrix. The automatic driver maybe ate (reward matrix) some electricity, renewable energy of course! The reward is a number such as 50 or 100 to show the agent that it's on the right track. It's like when a student gets a good grade in an exam.
- R(s): This is the sum of the values up to there. It's the total reward at that point.
- ϒ = gamma: This is here to remind us that trial and error has a price. We're wasting time, money, and energy. Furthermore, we don't even know whether the next step is right or wrong since we're in a trial-and-error mode. Gamma is often set to 0.8. What does that mean? Suppose you're taking an exam. You study and study, but you don't really know the outcome. You might have 80 out of 100 (0.8) chances of clearing it. That's painful, but that's life. This is what makes Bellman's equation and MDP realistic and efficient.
- max(s'): s' is one of the possible states that can be reached with Pa (s,s'); max is the highest value on the line of that state (location line in the reward matrix).