Matrix decompositions

The word decomposition means breaking something down into smaller parts. In this case, a matrix decomposition means breaking down a matrix into a sum of simpler matrices. By simpler matrices, we mean matrices whose properties are more convenient or efficient to work with. So, while a decomposition of a matrix still just gives us the same matrix, working with the component parts of the decomposition allows us to prove things more easily mathematically, such as derive a new algorithm, or to implement a calculation more efficiently in code.

We shall learn about two of the most important matrix decompositions in data science: the eigen-decomposition and the SVD. We won’t try to prove the decompositions – that is beyond the scope of this book. Instead, we shall state the decompositions and then show you their resulting properties and how they are useful.

Eigen-decompositions

We start with the eigen-decomposition of a square matrix. As this suggests, eigen-decompositions are limited to square matrices, that is, matrices that have the same number of rows as columns. Despite this limitation, eigen-decompositions are extremely useful because they allow us to understand the effect of a square matrix in terms of a set of simpler transformations that are independent of each other.

To explain the eigen-decomposition of a square matrix, we must first explain what the eigenvectors and eigenvalues of a matrix are.

Eigenvector and eigenvalues

If we have a square matrix , then an eigenvector of is a vector , which satisfies the following equation:

Eq. 35

The number is called an eigenvalue and is the eigenvalue associated with the eigenvector . An matrix will have eigenvectors, that is, solutions to Eq. 35, although it is possible that multiple of these eigenvectors will have the same eigenvalue, so there are or less distinct eigenvalues. By convention, eigenvectors are of unit length, that is, , since the length of any eigenvector that isn’t of unit length can just be absorbed into the eigenvalue.

So, what does Eq. 35 tell us? It tells us that the effect of on is to leave it untouched, except for the scaling by the constant . For many matrices , the eigenvectors form an orthonormal basis. We will assume that is the case from now on – see point 1 in the Notes and further reading section at the end of this chapter. So, now we can express any vector in terms of the eigenvectors of , and since we understand the effect of on each of these eigenvectors, understanding the effect of on is easy. Let’s make that explicit. We can represent any vector in terms of the eigenvectors , as follows:

Eq. 36

Since the eigenvectors are orthogonal to each other and of unit length, the coefficients in Eq. 36 are easy to calculate and are given by the formula , as we showed in Eq. 34. The effect of on is then easily calculated as follows:

Eq. 37

So, the effect of is simply to stretch or shrink along each of the eigenvectors. Whether we stretch or shrink along a particular eigenvector direction depends upon whether the magnitude of the corresponding eigenvalue is bigger or smaller than 1. We can think of the eigenvectors of as giving us a set of directions for an orthogonal coordinate system – the -dimensional equivalent of the plane. The values are just the coordinates of the point in this coordinate system, and the right-hand side of Eq. 37 tells us what happens to those coordinates when we apply the transformation to the point . Some of the coordinates increase in magnitude, some decrease in magnitude, and some get flipped if the corresponding eigenvalue is negative.

Eigen-decomposition of a square matrix

If we have an matrix and it has linearly independent eigenvectors, meaning we can’t write any eigenvector as a linear combination of the other eigenvectors, then we can write as follows:

Eq. 38

This is the eigen-decomposition of . Here, is an matrix whose columns are the eigenvectors of . The matrix is an diagonal matrix; the off-diagonal elements are all 0 and the diagonal element of is the eigenvalue .

Within data science, a lot of the matrices we deal with are derived from data, and so will be real-valued. This can make things simpler, particularly if our square matrix is also symmetric. A symmetric square matrix is one whose matrix elements satisfy , and so is equal to its own transpose, that is, .

For a real symmetric matrix , the inverse matrix is given by the transpose of , that is, . Firstly, this means that and is termed a unitary matrix because of this property. Secondly, it means we can write the eigen-decomposition as follows:

Eq. 39

If we write this out longhand in terms of the eigenvectors , we have the following:

Eq. 40

You’ll recall that the outer product gives a matrix, so the eigen-decomposition in Eq. 40 tells us we can write as a sum of simpler matrices, as follows:

Eq. 41

Since each of those matrices contains just the transformation along a single eigenvector, it represents a very simple transformation. Secondly, since all the eigenvectors are orthogonal to each other, the effect of is independent of the effect of when . When applying to a vector , it only affects the bit of that lies along eigenvector . This is the main benefit of the eigen-decomposition of the matrix. We have used the eigen-decomposition of to understand its effect by breaking down into a set of much simpler transformations that are easier to understand.

The sum in Eq. 40 also hints at another use of the eigen-decomposition. We can assume, without loss of generality, that the eigenvalues are ordered in magnitude, so that . An eigenvalue with a small magnitude will contribute very little to the sum in Eq. 40. This suggests we can approximate by truncating the summation in Eq. 40 to include only the largest-magnitude eigenvalues. Let’s say, for example, the first three eigenvalues were much bigger in magnitude than the others, then we could approximate the following:

Eq. 42

We shall see an example of this use of eigen-decompositions when we introduce PCA later in this chapter.

Our last point on the eigen-decomposition of a square matrix concerns the inverse matrix. Consider Eq. 38. Now let’s define another matrix, , constructed as . If we multiply by , we get the following:

Eq. 43

A similar calculation shows that . These two results tell us that is in fact the inverse matrix of (and vice versa). Now we already have the matrices , and from the eigen-decomposition of . So, to calculate the inverse of , all we need to do is calculate the inverse of the diagonal matrix . Calculating the inverse of a diagonal matrix is easy – we just take the ordinary reciprocal of the diagonal matrix elements. So, is also diagonal and its diagonal element is . So, the inverse of can be written as follows:

Eq. 44

The first thing to notice is that we can only do the calculation in Eq. 44 if we can take the reciprocal of each of the eigenvalues . If any of the eigenvalues are 0, then we can’t perform this calculation and the inverse of does not exist. This is what we meant when we introduced the definition of the inverse matrix and said that some square matrices do not have an inverse.

The second thing to notice is when we have a real symmetric matrix. If is real and symmetric, then, as we have said, its eigen-decomposition takes the simpler form . As you might expect, its inverse matrix is then , provided, of course, that none of the eigenvalues are 0. This means that we can write out in longhand, as a sum of simpler matrices, just as we did in Eq. 40, and we get the following:

Eq. 45

So, just as Eq. 40 helped us understand what the transformation represented, Eq. 45 helps us understand what represents.

Let’s look at how to calculate an eigen-decomposition of a square matrix with a code example.

Eigen-decomposition code example

Once again, we’ll use the in-built functions in the NumPy package to do this. All the following code examples (and additional ones) can be found in the Code_Examples_Chap3.ipynb Jupyter notebook in the GitHub repository.

Eigen-decomposition of a square array can be done using the numpy.linalg.eig function. However, since in this code example we’ll focus on calculating the eigen-decomposition of a real symmetric matrix, we can use the more specific numpy.linalg.eigh function:

import numpy as np
# Create a 4x4 symmetric square matrix
A = np.array( [[1, 2, 3, 4],
               [2, 1, 2, 1],
               [3, 2, 3, 2],
               [4, 1, 2, 2]])
# Calculate the eigen-decomposition
eigvals, eigvecs = np.linalg.eigh(A)

eigvals is a NumPy array that holds the eigenvalues. The eigenvalues are shown here:

array([-2.84382794, -0.22727708, 1.02635, 9.04475502])

We can also check that the eigenvectors are orthogonal to each other:

# Check that the eigenvectors are orthogonal to each other
# and are of unit length. We can do this by calculating the
# inner product for each pair of eigenvectors
for i in range(A.shape[0]):
     for j in range(i,A.shape[0]):
         print("i=",i, "j=",j, "Inner product = ", 
               np.inner(eigvecs[:, i], eigvecs[:, j]))

This gives the following output:

i= 0 j= 0 Inner product =  1.0
i= 0 j= 1 Inner product =  -2.7755575615628914e-17
i= 0 j= 2 Inner product =  -5.551115123125783e-17
i= 0 j= 3 Inner product =  -1.6653345369377348e-16
i= 1 j= 1 Inner product =  1.0
i= 1 j= 2 Inner product =  5.551115123125783e-17
i= 1 j= 3 Inner product =  0.0
i= 2 j= 2 Inner product =  0.9999999999999993
i= 2 j= 3 Inner product =  -8.326672684688674e-17
i= 3 j= 3 Inner product =  0.9999999999999999

That code example concludes our explanation of the eigen-decomposition of a square matrix, so we’ll now move on to another important matrix decomposition technique.

Singular value decomposition

The eigen-decomposition works for square matrices. What happens if our matrix is not square? Are there any matrix decompositions for non-square matrices that break the matrix down into orthonormal vectors? The answer is yes. Any matrix, whether square or otherwise, has an singular value decomposition (SVD).

We will initially restrict ourselves to real matrices. Again, in a data science setting, this is not too much of a restriction as most of the matrices you will encounter will be data-related and hence real. We will return to the more general case of complex matrices later. The SVD of a real matrix that has (more rows than columns) is given as follows:

Eq. 46

This decomposition is shown schematically in Figure 3.5.

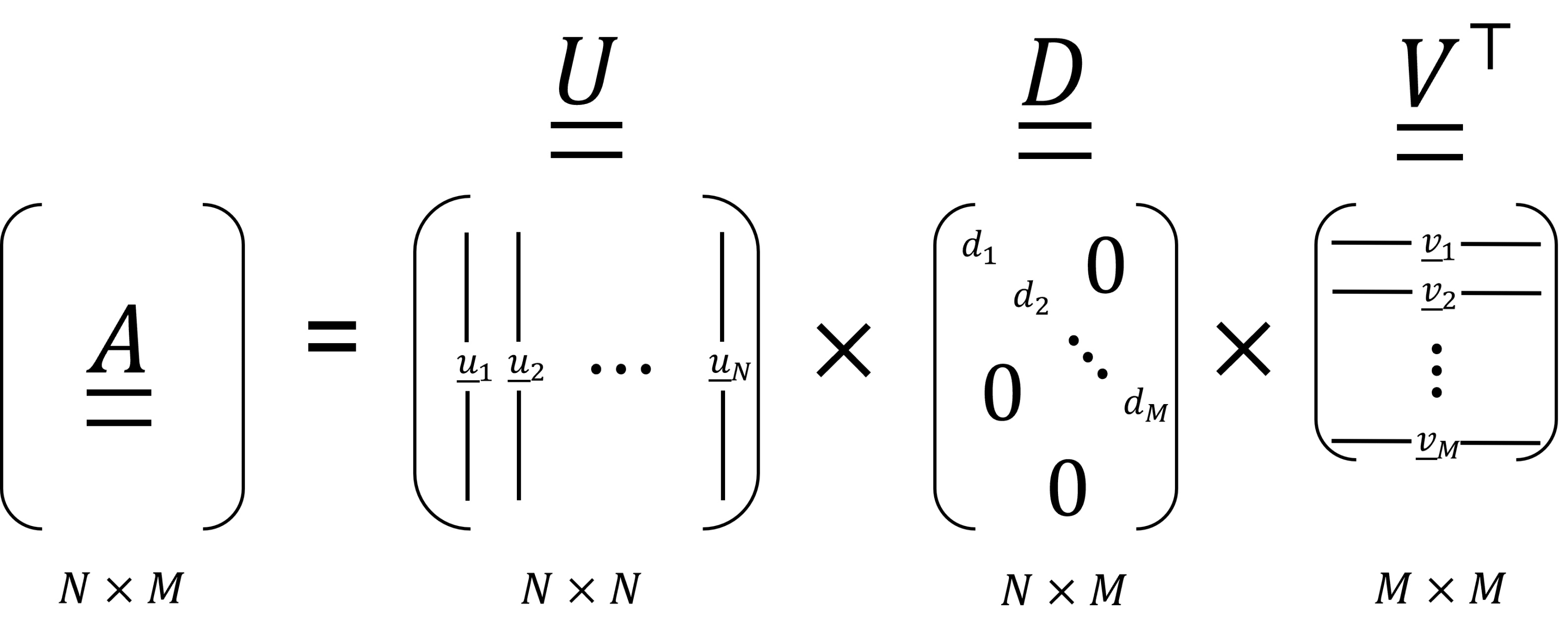
Figure 3.5: The SVD of a real-valued matrix

Here, is an matrix whose columns are a set of orthonormal vectors, , so that for all and for . In fact, the matrix is unitary, so . The vectors are known as the left singular vectors of .

Likewise, the matrix is an matrix whose columns are a set of orthonormal vectors , so that for all , and if . is also a unitary matrix, so . The vectors are known as the right singular vectors of .

The matrix is a diagonal matrix – all the off-diagonal elements are 0. Matrix has values on its leading diagonal. The diagonal element of is and is called the singular value.

Okay, the preceding explanation is the textbook definition. Let’s unpack the SVD a bit further to understand what the singular vectors and singular value represent. We’ll look at the symmetric matrix . Using the SVD of , we can write this as follows:

Eq. 47

Here, we have used the fact that the transpose of the product of matrices is the same as taking the product of the transposes, but with the order reversed, that is, . Now, if you also recall that since the columns of are a set of orthonormal vectors, then , and so we have the following:

Eq. 48

Since is a diagonal matrix, the matrix is an diagonal matrix, and so by comparing it to Eq. 39, we can recognize Eq. 48 as the eigen-decomposition of the square matrix . So, the left singular vectors, , are also eigenvectors of the matrix .

A similar calculation, where we consider the symmetric matrix , shows the following:

Eq. 49

With being an diagonal matrix, we recognize Eq. 49 as an eigen-decomposition and so the right singular vectors, , are also eigenvectors of . So, in a similar way to what we did with the eigen-decomposition of a matrix, it helps to write out the SVD in a longhand form:

Eq. 50

The first thing to notice is that because we only have singular values, the sum in Eq. 50 is restricted to just terms and only the first left singular vectors contribute. This means that sometimes you will see the SVD of a matrix defined in a more compact form, with being an matrix whose columns are , and being an diagonal matrix whose diagonal elements are . This slightly more compact form of the SVD is shown schematically in Figure 3.6.

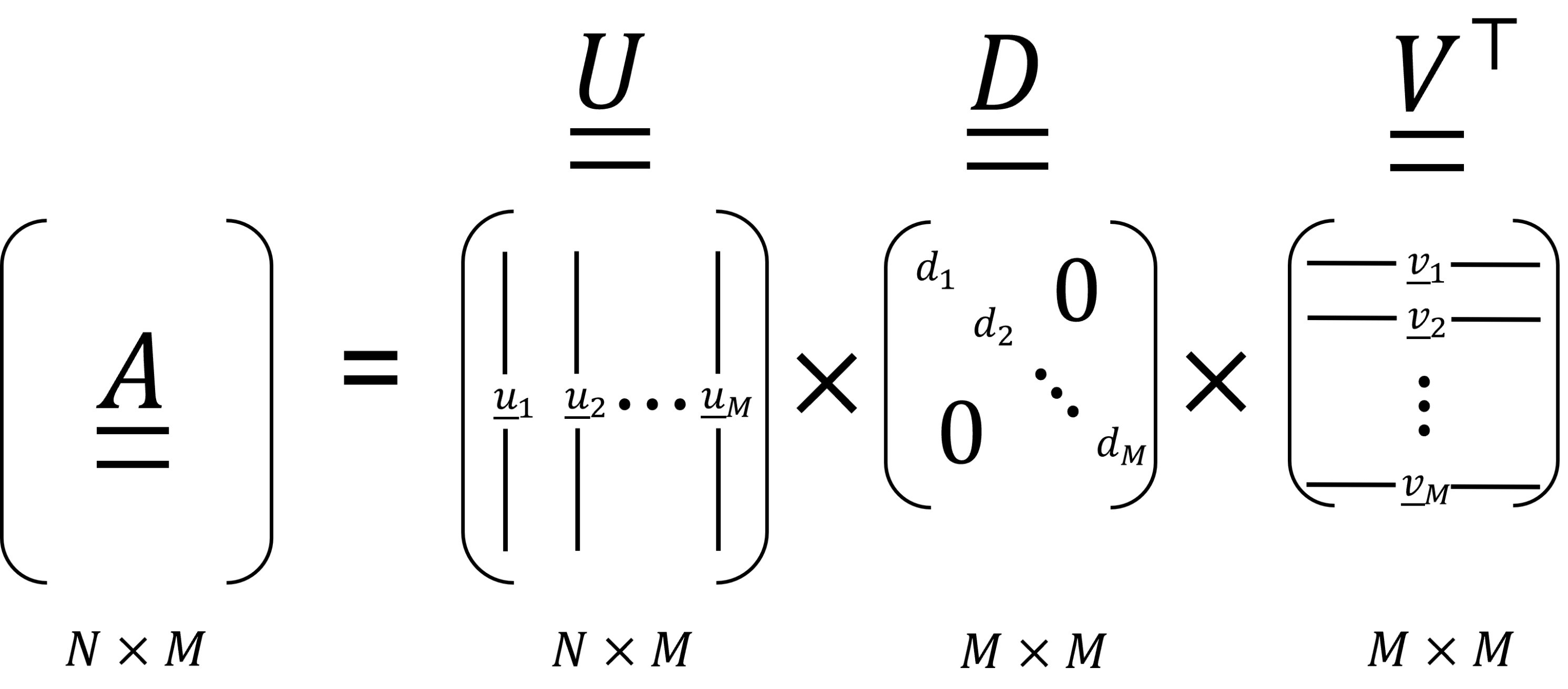
Figure 3.6: The compact form of the SVD of a real-valued matrix

Secondly, we can see that Eq. 50 allows us to write as a sum of independently acting matrices,

Eq. 51

The individual matrix contains just the transformation from the left and right singular vector pair . Applying to a vector is easily calculated and is given by the following:

Eq. 52

Since the vectors and are unit length, Eq. 52 tells us that the effect of on is to project onto and use the result of that projection to output a scaled version of the left singular vector . Also, since each left singular vector is orthogonal to every other left singular vector, and each right singular vector is orthogonal to every other right singular vector, this means each matrix acts in an orthogonal fashion, that is, independently of the others. Just as the eigen-decomposition helps us to understand a square matrix, the SVD of allows us to understand more easily the effect of the transformation that represents.

As with the eigen-decomposition, the larger the magnitude of the singular value , the more important the corresponding pair of left and right singular vectors in the sum in Eq. 50. The SVD of shows us how we can approximate by truncating the sum in Eq. 50 to just the largest-magnitude singular values.

The SVD of a complex matrix

So far, we have restricted our discussion of the SVD to real matrices, since those are most of the matrices we encounter as data scientists. Let’s now return to a general matrix, that is, one that potentially contains matrix elements that are complex numbers. For such matrices, we still have an SVD. For a general matrix , its SVD is as follows:

Eq. 53

In this more general form, and are complex unitary matrices. Also, the other new aspect here is that we have instead of . What is this new symbol? What does represent? It is called the Hermitian conjugate of the matrix . The Hermitian conjugate is also the conjugate transpose of , obtained by taking the transpose of and then taking the complex conjugate of each matrix element. The order of those operations can be reversed, that is, take the complex conjugate of each element of and then the transpose – the combined result is the same.

We’ll finish our explanation of the SVD with a code example. We’ll look at how to calculate the SVD of a real-valued matrix.

SVD code example

For our code example, we’ll again make use of the in-built functions in the NumPy package to do this. The following code example (and additional ones) can be found in the Code_Examples_Chap3.ipynb Jupyter notebook in the GitHub repository.

We’ll use the numpy.linalg.svd function to perform the SVD. This function has a full_matrices Boolean argument, which, when set to False, computes the compact form of the SVD shown in Figure 3.6, with the smaller form of the matrix . When full_matrices is set to True, we get the full form of the SVD shown in Figure 3.5. We’ll calculate both forms of the SVD for a real matrix . We start by creating the matrix :

import numpy as np
# Create a 5x3 matrix
A = np.array([[1.0, 2.0, 3.0],
              [-1.0, 0.0, 1.0],
              [3.0, 3.0, 2.0],
              [2.0, 4.0, 7.0],
              [1.0, -0.5, -2.0]])

Now, we can calculate the full SVD of the matrix. Calling the numpy.linalg.svd function returns a triple of arrays corresponding to the , and matrices. This is shown here:

# Calculate SVD. In this instance the matrix
# u will be a square matrix with the same number of rows
# as the input matrix A has
u, d, v_transpose = np.linalg.svd(A, full_matrices=True)

We can also calculate the compact form of the SVD by simply changing the value of the full_matrices argument. This is shown here:

# Calculate the compact form of the SVD. In this instance
# the matrix u_compact will have the same shape as the input
# matrix A
u_compact, d_compact, v_transpose_compact = np.linalg.svd(
    A, full_matrices=False)

Let’s check that the two different SVD calculations do indeed have different shapes for the matrix . We do this as follows:

# Let's check that the matrix U has different shapes in
# compact and non-compact forms of the SVD
print(u.shape, u_compact.shape)

This gives the following output:

(5, 5) (5, 3)

With that short code example, we’ll end our explanation of the SVD. It is time to recap what we have learned about matrix decompositions.

What we learned

In this section, we have learned the following:

• About the eigenvectors and eigenvalues of a square matrix
• How to calculate the eigen-decomposition of a square matrix
• How the eigen-decomposition of a square matrix provides us with a simpler way to understand the transformation represented by real symmetric square matrices
• How to calculate the SVD of a matrix
• How the SVD of a matrix gives us a simpler way to understand the transformation represented by any matrix

Having learned about the two most important decomposition methods that can be applied to matrices, we will learn about some key metrics or properties that are used to summarize square matrices and how those metrics are calculated in terms of the eigenvalues of the matrix.