Language models
In terms of natural language processing, language models generate output strings that help to assess the likelihood of a bunch of strings to be a sentence in a specific language. If we discard the sequence of words in all sentences of a text corpus and basically treat it like a bag of words, then the efficiency of different language models can be estimated by how accurately a model restored the order of strings in sentences. Which sentence is more likely: I am learning text mining or I text mining learning am? Which word is more likely to follow I am…?
Language models are widely used in machine translation, spelling correction, speech recognition, text summarization, questionnaires, and so on.
Basically, a language model assigns the probability of a sentence being in a correct order. The probability is assigned over the sequence of terms by using conditional probability. Let us define a simple language modeling problem. Assume a bag of words contains words W1, W2,………………….,Wn.. A language model can be defined to compute any of the following:
- Estimate the probability of a sentence S1: P (S1) = P (W1, W2, W3, W4, W5)
- Estimate the probability of the next word in a sentence or set of strings:
P (W3|W2, W1)
How to compute the probability? We will use chain law, by decomposing the sentence probability as a product of smaller string probabilities:
P(W1W2W3W4) = P(W1)P(W2|W1)P(W3|W1W2)P(W4|W1W2W3)
N-gram models
N-grams are important for a wide range of applications. They can be used to build simple language models. Let's consider a text T with W tokens. Let SW be a sliding window. If the sliding window consists of one cell 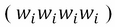 then the collection of strings is called a unigram; if the sliding window consists of two cells, the output is
then the collection of strings is called a unigram; if the sliding window consists of two cells, the output is 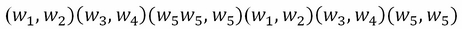 , this is called a bigram .Using conditional probability, we can define the probability of a word having seen the previous word; this is known as bigram probability. So the conditional probability of an element, , given the previous element,
, this is called a bigram .Using conditional probability, we can define the probability of a word having seen the previous word; this is known as bigram probability. So the conditional probability of an element, , given the previous element,  is:
is:

Extending the sliding window, we can generalize that n-gram probability as the conditional probability of an element given previous n-1 element:

The most common bigrams in any corpus are not very interesting, such as on the, can be, in it, it is. In order to get more meaningful bigrams, we can run the corpus through a part-of-speech (POS) tagger. This would filter the bigrams to more content-related pairs such as infrastructure development, agricultural subsidies, banking rates; this can be one way of filtering less meaningful bigrams.
A better way to approach this problem is to take into account collocations; a collocation is the string created when two or more words co-occur in a language more frequently. One way to do this over a corpus is pointwise mutual information (PMI).The concept behind PMI is for two words, A and B, we would like to know how much one word tells us about the other. For example, given an occurrence of A, a, and an occurrence of B, b, how much does their joint probability differ from the expected value of assuming that they are independent. This can be expressed as follows:

- Unigram model:
Punigram(W1W2W3W4) = P(W1)P(W2)P(W3)P(W4)
- Bigram model:
Pbu(W1W2W3W4) = P(W1)P(W2|W1)P(W3|W2)P(W4|W3) P(w1w2…wn ) = P(wi | w1w2…wi"1)
Applying the chain rule on n contexts can be difficult to estimate; Markov assumption is applied to handle such situations.
Markov assumption
If predicting that a current string is independent of some word string in the past, we can drop that string to simplify the probability. Say the history consists of three words, Wi, Wi-1, Wi-2, instead of estimating the probability P(Wi+1) using P(Wi,i-1,i-2) , we can directly apply P(Wi+1 | Wi, Wi-1).
Hidden Markov models
Markov chains are used to study systems that are subject to random influences. Markov chains model systems that move from one state to another in steps governed by probabilities. The same set of outcomes in a sequence of trials is called states. Knowing the probabilities of states is called state distribution. The state distribution in which the system starts is the initial state distribution. The probability of going from one state to another is called transition probability. A Markov chain consists of a collection of states along with transition probabilities. The study of Markov chains is useful to understand the long-term behavior of a system. Each arc associates to certain probability value and all arcs coming out of each node must have exhibit a probability distribution. In simple terms, there is a probability associated to every transition in states:
.

Hidden Markov models are non-deterministic Markov chains. They are an extension of Markov models in which output symbol is not the same as state. We will discuss this topic in detail in later chapters.























































