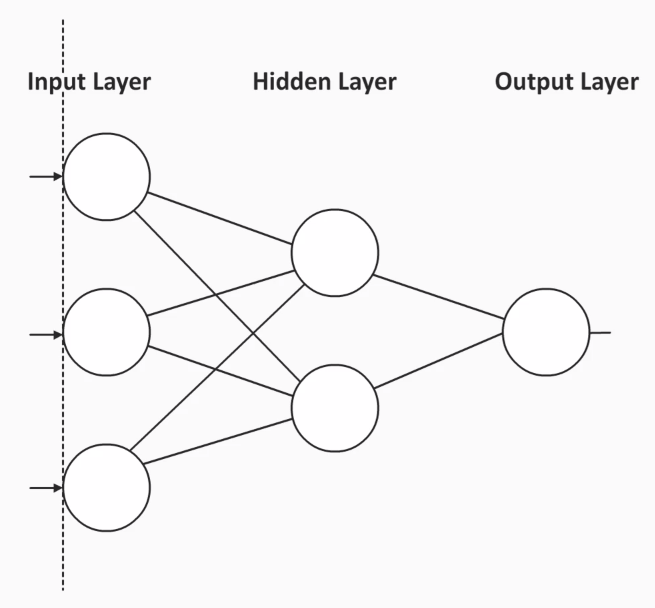
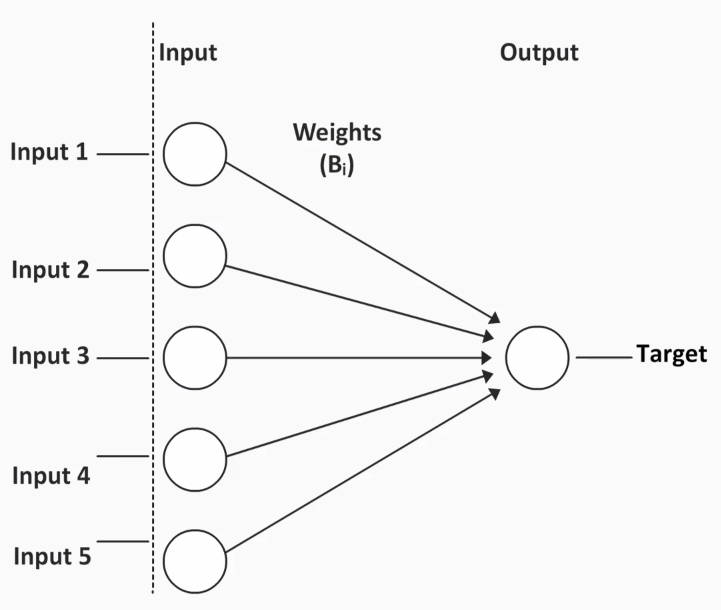
Neural networks were initially developed in an attempt to understand how the brain operates. They were originally used in the areas of neuroscience and linguistics.
In these fields, researchers noticed that something happened in the environment (input), the individual processed the information (in the brain), and then reacted in some way (output).
So, the idea behind neural networks or neural nets is that they will serve as a brain, which is like a black box. We then have to try to figure out what is going on so that the findings can be applied.