The most basic element that we will deal with is called the neuron. If we were to take the most basic form of an activation function that a neuron would use, we would have a function that has only two possible results, 1 and 0. Visually, such a function would be represented like this:
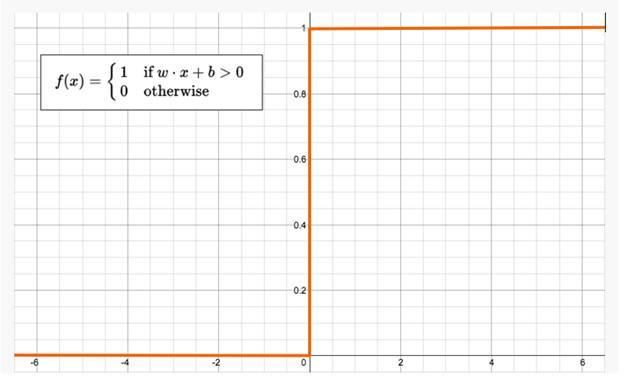
This function returns 1 if the input is positive or 0, otherwise it returns 0. A neuron whose activation function is like this is called a perceptron. It is the simplest form of neural network we could develop. Visually, it looks like the following:
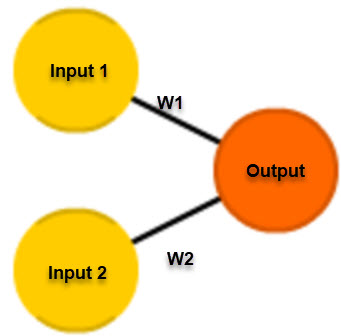
The perceptron follows the feed-forward model, meaning inputs are sent into the neuron, processed, and then produce output. Inputs come in, and output goes out. Let's use an example.
Let's suppose that we have a single perceptron with two inputs as shown previously. For the purposes of this example, input 0 will be x1 and input 1 will be x2. If we assign those two variable values, they will look something like this:
Input 0: x1 = 12
Input 1: x2 = 4
Each of those inputs must be weighted, that is, multiplied by some value, which is often a number between -1 and 1. When we create our perceptron, we begin by assigning them random weights. As an example, Input 0 (x1) will have a weight we'll label w1, and input 1, x2 will have a weight we'll label w2. Given this, here's how our weights look for this perceptron:
Weight 0: 0.5
Weight 1: -1
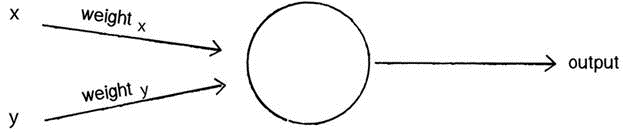
Once the inputs are weighted, they now need to be summed. Using the previous example, we would have this:
6 + -4 = 2
That sum would then be passed through an activation function, which we will cover in much more detail in a later chapter. This would generate the output of the perceptron. The activation function is what will ultimately tell the perceptron whether it is OK to fire, that is, to activate.
Now, for our activation function we will just use a very simple one. If the sum is positive, the output will be 1. If the sum is negative, the output will be -1. It can't get any simpler than that, right?
So, in pseudo code, our algorithm for our single perceptron looks like the following:
- For every input, multiply that input by its weight
- Sum all the weighted inputs
- Compute the output of the perceptron based on that sum passed through an activation function (the sign of the sum)


























































