In both supervised and unsupervised learning problems, there will always be a dataset, defined as a finite set of real vectors with m features each:
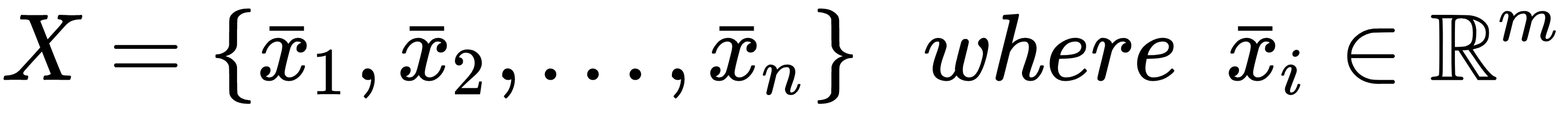
Considering that our approach is always probabilistic, we need to assume each X as drawn from a statistical multivariate distribution, D, that is commonly known as a data generating process (the probability density function is often denoted as pdata(x)). For our purposes, it's also useful to add a very important condition upon the whole dataset X: we expect all samples to be independent and identically distributed (i.i.d). This means that all variables belong to the same distribution, D, and considering an arbitrary subset of k values, it happens that the following is true:
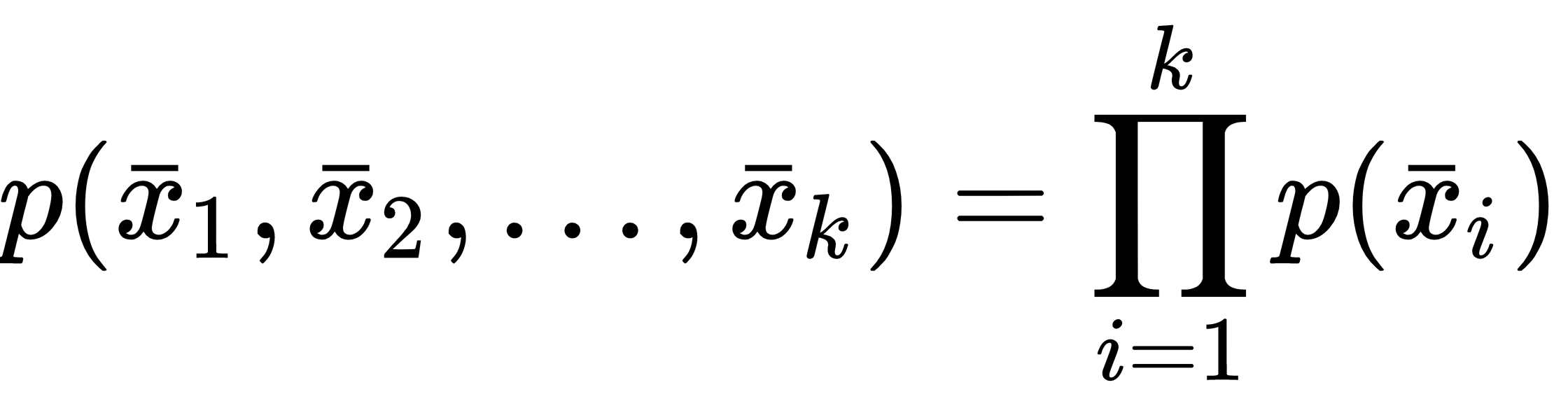
It's fundamental to understand that all machine learning tasks are based on the assumption of working with well-defined distributions...












































































