Generating full factorial designs
Often in scientific computing, we are interested in generating a full factorial design of a computational experiment (see, for example, http://www.socialresearchmethods.net/kb/expfact.php or https://en.wikipedia.org/wiki/Factorial_experiment). A typical application of this design is performing a grid search in hyperparameter tuning of machine learning models (see https://cloud.google.com/ml-engine/docs/tensorflow/hyperparameter-tuning-overview or https://en.wikipedia.org/wiki/Hyperparameter_optimization#Grid_search).
Assume that we are given a list of vectors and we want to generate all possible combinations of values taken from those vectors. For instance, if we have the x=[1,2] and y=['a', 'b']vectors, we have four possible combinations of values taken from them, namely, (1,'a'), (2, 'a'), (1,'b'), and (2,'b'). In general, if we have
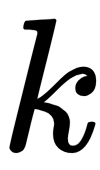
vectors, and vector
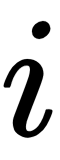
has
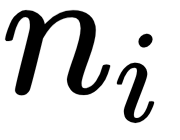
elements, then there are
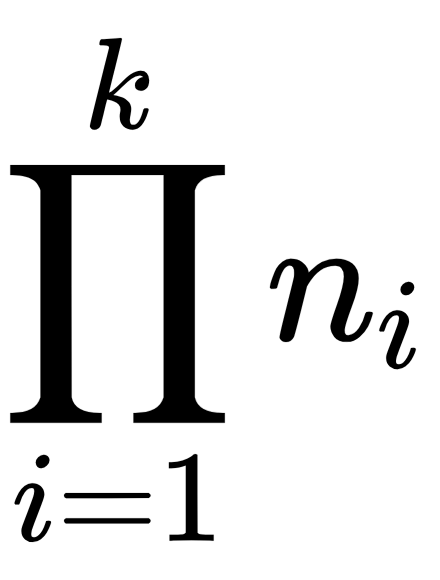
such combinations. In this recipe, we will show how to use the matrix...





































































