Bayes' theorem
The conditional probability formula is:

where E and F are any events (that is, sets of outcomes) with positive probabilities. If we swap the names of the two events, we get the equivalent formula:
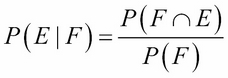
But F ∩ E = E ∩ F, so P(F ∩ E) = P(E ∩ F) = P(F│E) P(E). Thus:

This formula is called Bayes' theorem. The main idea is that it reverses the conditional relationship, allowing one to compute P(E│F) from P(F│E).
To illustrate Bayes' theorem, suppose the records of some Health Department show this data for 1,000 women over the age of 40 who have had a mammogram to test for breast cancer:
80 tested positive and had cancer
3 tested negative, but had cancer (a Type I error)
17 tested positive, but did not have cancer (a Type II error)
900 tested negative and did not have cancer
Notice the designations of errors of Type I and II. In general, a Type I error is when a hypothesis or diagnosis is rejected when it should have been accepted (also called a false negative), whereas a Type II error is when...



































































