5.3 Linear maps

We’ve looked at linear functions several times to get a concrete idea of how they work. We must generalize this idea to vector spaces.

Let U and V be vector spaces over the same field F. Let u₁ and u₂ be in U and s₁ and s₂ be scalars in F.

The function L: U → V is a linear map if

In particular, we have

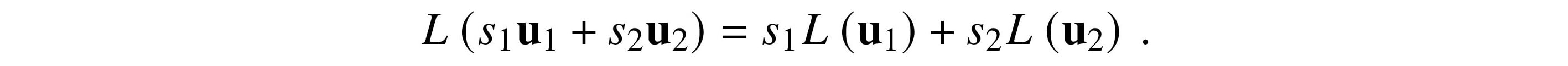
When U = V, we also say L is a linear transformation of U or a linear operator on U. linear$map linear$transformation linear$operator

All linear transformations on R² look like

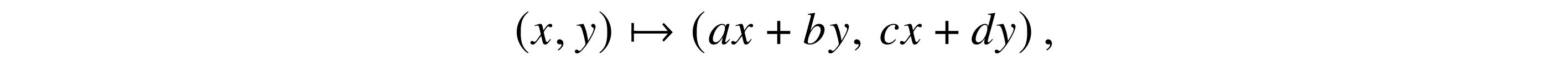
using Cartesian coordinates, and with a, b, c, d, x, and y in R. This is interesting because the linear transformations on R¹ all look like the somewhat trivial x ↦ ax.

Exercise 5.2

Show that the function

for a, b, c, d, x, and y in C is a linear transformation of C².

The linear transformations on R^3...