How do instruments create sound with different pitches?
In order to understand how instruments create pitches, we need to understand how instruments create sound waves. There are two types of sound waves. Traveling waves are observed when a wave is not confined to a given space. If you were to shake an unattached, loose rope, the resulting random ripple in the rope would be a traveling wave. The wave could have any wavelength as there’s nothing restricting the length.
Standing waves, on the other hand, occur when a wave is confined to a fixed space in a medium. The medium restricts the wavelength to hit recurring wavelengths and frequencies. If you were to shake a string that’s attached to a pole, the resulting constrained ripple would be a standing wave.
This medium restriction produces a regular wave pattern that repeats. We call this a standing wave (as though it were standing still). You can see an example of a standing wave in the following figure:
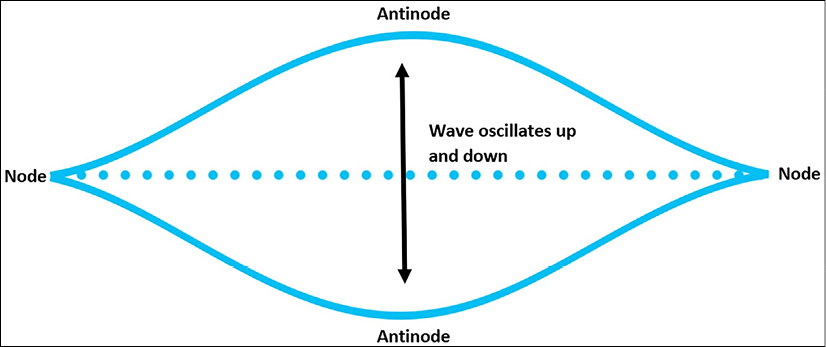
Figure 5.4 – Standing wave
You can think of a standing wave as a guitar string. The string is attached to both ends of the guitar and so each string end has no movement. Only the middle of the string can move. Physicists call the point of no movement on a wave a node. The part of a wave that moves is called the antinode. The wave appears to vibrate in a repeating movement where only the amplitude of the wave is changing.
If you tune a guitar, it will tighten the string, restrict the wavelength, and cause the string to vibrate a certain number of times per second. What you’re doing by tuning the guitar string is shaping the frequency of the wave. When you hear the frequency of the wave, you recognize the sound as a specific pitch. When you press down on the guitar string in different places, you cause the active part of the string to change lengths, resulting in a new note pitch.
In wind and brass instruments, there are no strings to vibrate. Instead, the air molecules are restricted within the space of the pipe. This space confines the size of the wavelength and amplitude. The shape of the pipe dictates the nature of the standing wave. The following figure shows a wave confined within a pipe:
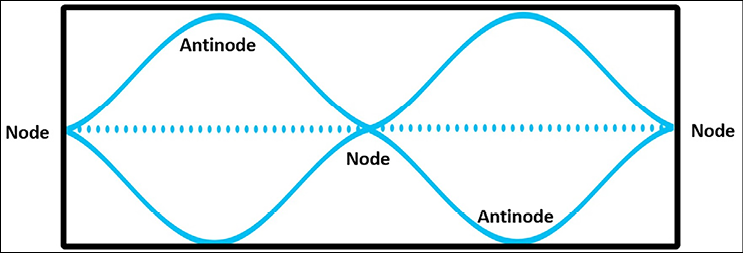
Figure 5.5 – Standing wave in a pipe
In a pipe (like a woodwind or brass instrument), the end of the pipe acts as the fixed node. The wave reflects back off the end of the pipe and creates the waveform. An open-ended pipe can reflect a wave too, even if there isn’t a solid surface for the wave to reflect off.
There are a number of variables to play around with that can shape the wave, such as how long the pipe is, whether the pipe is open or closed, and how many openings are open or closed. Imagine a flute. When you blow into a flute, the sound changes depending on how many holes you cover. The pitch is dictated by the number of open holes.
If we adjust the medium the wave is traveling through (such as making the pipe longer or shorter), we can get a different number of wave nodes and antinodes. This is a way to change the pitch we hear. The lowest number of nodes and antinodes that can exist in a wave is two nodes and one antinode. We call this the first harmonic, also known as the fundamental:
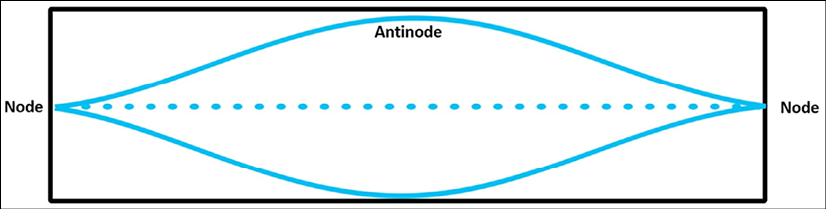
Figure 5.6 – First harmonic (fundamental)
If we add a single node and antinode to our wave, we get a wave like the one in the following figure. You can see that there are now three nodes and two antinodes:
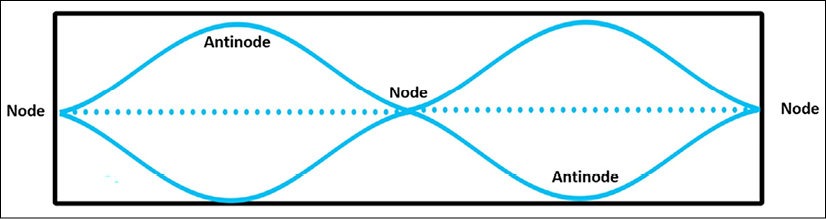
Figure 5.7 – Second harmonic (first overtone)
We call this the second harmonic. Another name for this is the first overtone. Music theory often uses the term harmonic. Physics often uses the term overtone, but they both mean the same thing. Notice we have increased the frequency of the wave. The first harmonic only had half a wavelength, while the second harmonic has a full wavelength, but it’s the same total distance. This means the pitch of the sound would be higher. How much higher? Exactly one octave. If, for example, our fundamental had a pitch of middle C, meaning it had a frequency of 261.6 Hz, the second harmonic/first overtone would be 523.2 Hz, or a C note that is exactly one octave higher.
If we add another node and antinode, we get a wave as in the following screenshot:
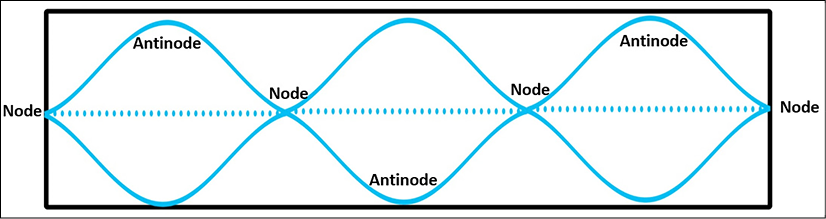
Figure 5.8 – Third harmonic (second overtone)
A wave with four nodes and three antinodes is known as the third harmonic, also known as the second overtone. Note that the frequency has increased again; the amount would again be another octave higher.
What all of this means is that instruments can create different pitches by modifying the sound wavelength and frequency of the wave.































































