Now that we've seen a few examples of how GNNs work, let's go a step further and see how we can apply neural networks to meshes.
First, we use a patch that is defined at each point in a local system of d-dimensional pseudo-coordinates,  , around x. This is referred to as a geodesic polar. On each of these coordinates, we apply a set of parametric kernels,
, around x. This is referred to as a geodesic polar. On each of these coordinates, we apply a set of parametric kernels,  , that produces local weights.
, that produces local weights.
The kernels here differ in that they are Gaussian and not fixed, and are produced using the following equation:
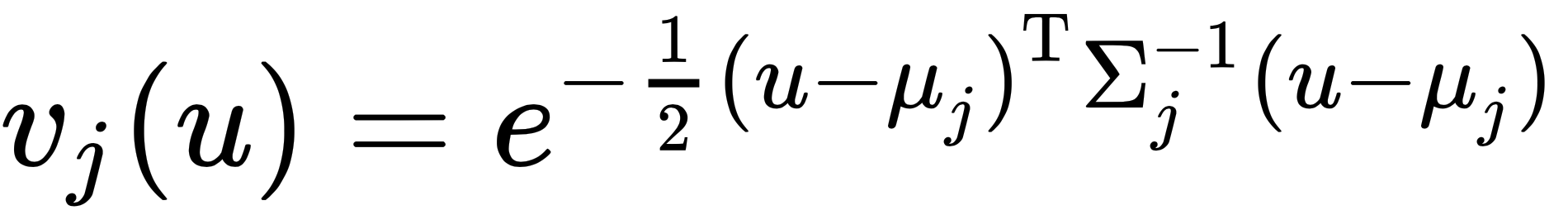
These parameters ( and
and  ) are trainable and learned.
) are trainable and learned.
A spatial convolution with a filter, g, can be defined as follows:
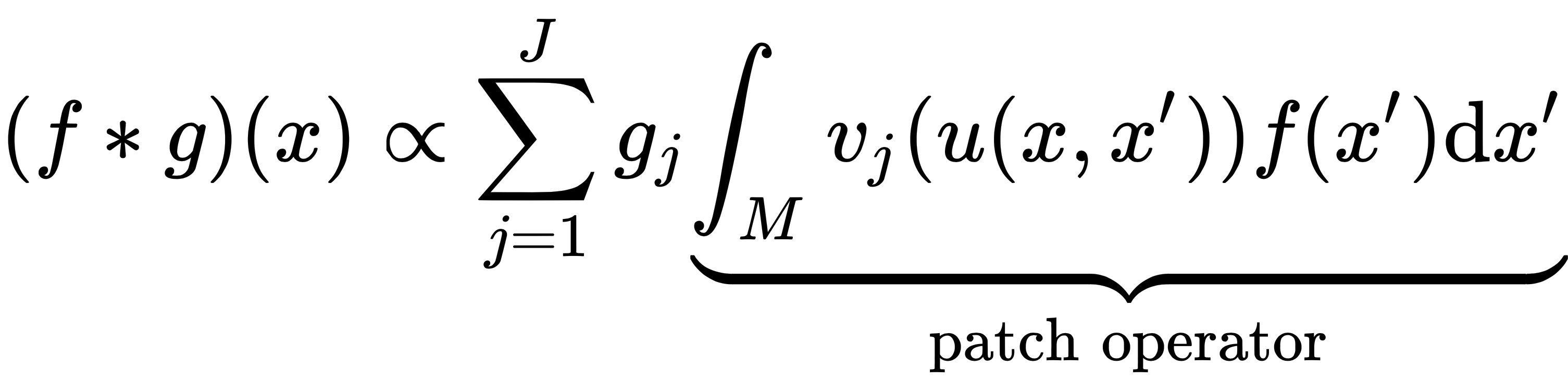
Here,  is a feature at vertex i.
is a feature at vertex i.
Previously, we mentioned geodesic polar coordinates, but what are they? Let's define them and find out. We can write them as follows:
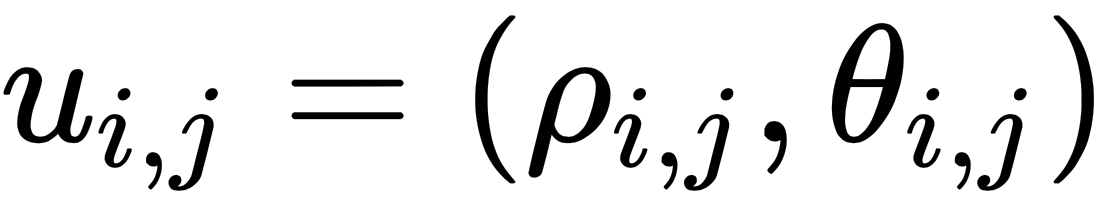
Here,  is the geodesic distance between i and j and
is the geodesic distance between i and j and  is the...
is the...












































































