Exploring time series properties and examples
A general definition of a time series is the following:
This definition highlights two fundamental aspects of a time series: the fact that observations are a function of time and that, as a consequence of this fact, some typical temporal features are often observed. The fluctuations and the long period direction of the series are just some of these features, as there might be other relevant aspects to take into consideration such as autocorrelation, stationarity, and the order of integration. We will explore these aspects in more detail in future chapters. In this section, we will focus on the distinction between discrete time series and continuous time series, on the concept of independence between observations, and finally, we will show some examples of real-world time series.
Continuous and discrete time series
A Time Series is defined as continuous when observations are collected continuously over time, that is, there can be an infinite number of observations in a given time range. Typically, continuous time series data is sampled at irregular time intervals. Consider the measurement of a patient’s blood pressure in a hospital done at varying time points during the day, not equally spaced. This happens because, in some settings, regular monitoring at fixed intervals is not possible. For instance, in Figure 1.1, there are four medical continuous time series, relative to the health parameters of four patients:
- Mean blood pressure
- Heart rate
- Temperature
- Glucose data
As evident from the graphs, there are some temporal ranges where the measures are not present, for example, the temperature and glucose between approximately 20 hours and 30 hours of the monitoring period. There are other time points where data is collected more frequently than in other periods. These time series features are due to the fact that the data has been collected manually by the physician or by the nurse, not at fixed moments of the day. Therefore, this type of time series is inherently irregularly sampled:
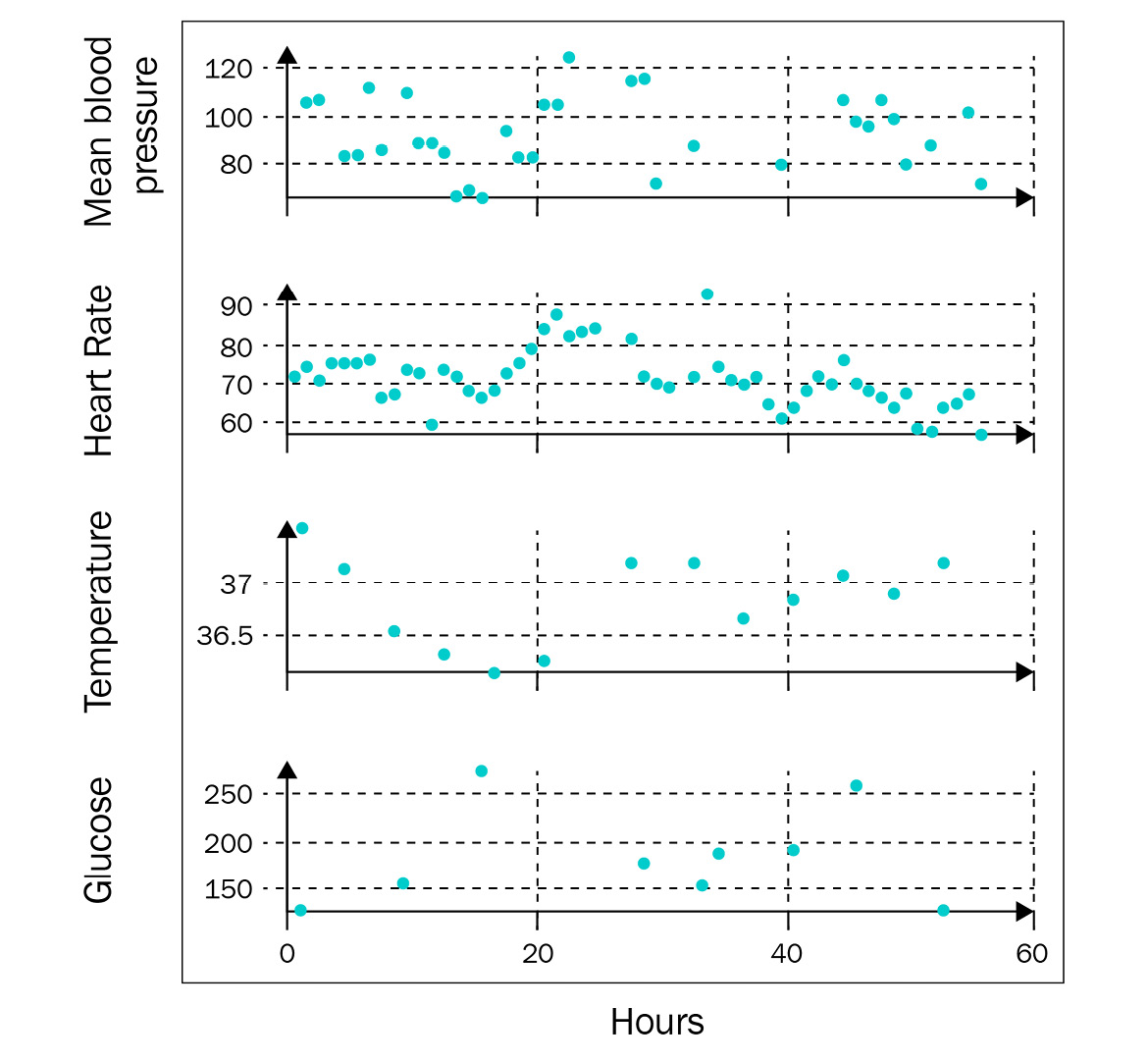
Figure 1.1 – Four continuous, irregularly sampled, medical time series
A time series is defined as discrete when observations are collected regularly at specific times, typically equally spaced (that is, hourly, daily, weekly, and yearly data points).
A time series of this type can be natively discrete, such as the annual budget data of a company, or it can be created through the aggregation or accumulation of a numerical variable in equal time intervals. For example, the monthly sales of a supermarket or the number of daily passengers in a train station. A continuous time series can be discretized by binning/grouping the original data and, eventually, obtaining a discrete time series.
Classical TSA focuses on discrete time series because they are more common in real-world applications and easier to analyze. Therefore, in this book, we mainly deal with discrete time series, where observations are collected at equal intervals. When we consider irregularly sampled time series, first, we will try to transform them into regularly sampled data points.
Independence and serial correlation
One of the most distinctive characteristics of a time series is the mutual dependence between the observations, generally called serial correlation or autocorrelation.
In many statistical models, observations are assumed to be generated by a random sampling process and to be independent of each other (consider the linear regression model). Typically, this assumption turns out to be inconsistent with time series data, where simply collecting the data sequentially, along the time axis, generally produces observations that are not independent of each other.
Think of the daily sales of an e-commerce company. It’s reasonable to imagine that today’s sales are somehow related to the previous day’s sales: successive observations are dependent. However, in this context, which clearly can create some problems in using classical statistical tools, it is however possible to exploit the temporal dependence of observations to improve the forecasting process. If today’s sales are related to yesterday’s, and we can consistently estimate this relationship, then we can improve the forecast of tomorrow’s sales based on today’s result.
Time series examples
Interesting examples of time series can be collected in a multitude of information domains: business/economics, industrial production, social sciences, physics, and more. The time series obtained from these fields might be profoundly different in terms of statistical properties and the granularity of the available data, yet the methodologies of descriptive analysis and forecasting are essentially the same.
Here, we will explore a line chart (also called a time plot) of some representative discrete time series, with the aim of showing how it is possible to observe very different dynamics, depending on the type of data and the field of reference. Figure 1.2 shows the pattern of two annual time series, that is, the Number of PhDs awarded in the US, split between the subjects of engineering and education:
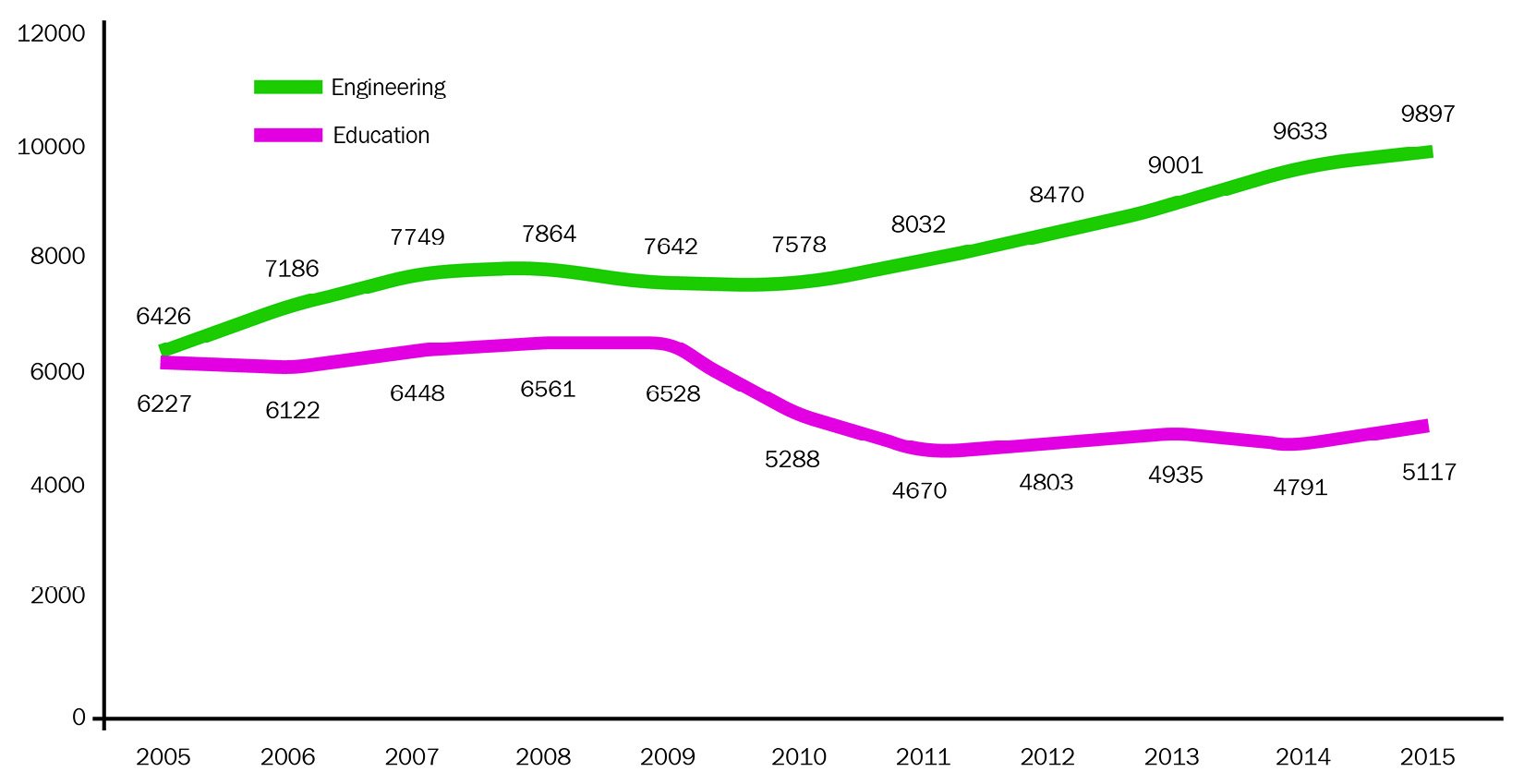
Figure 1.2 – Time series example 1: number of PhDs awarded in the US, showing the annual data for Engineering versus Education
In the preceding graph, we can see that both time series do not show periodic fluctuations, and this is typical of annual data. The engineering doctorate series appears to be increasing over time, especially in the last 5 years presented, while the education doctorate series shows a flatter trend, with a level shift between 2010 and 2011.
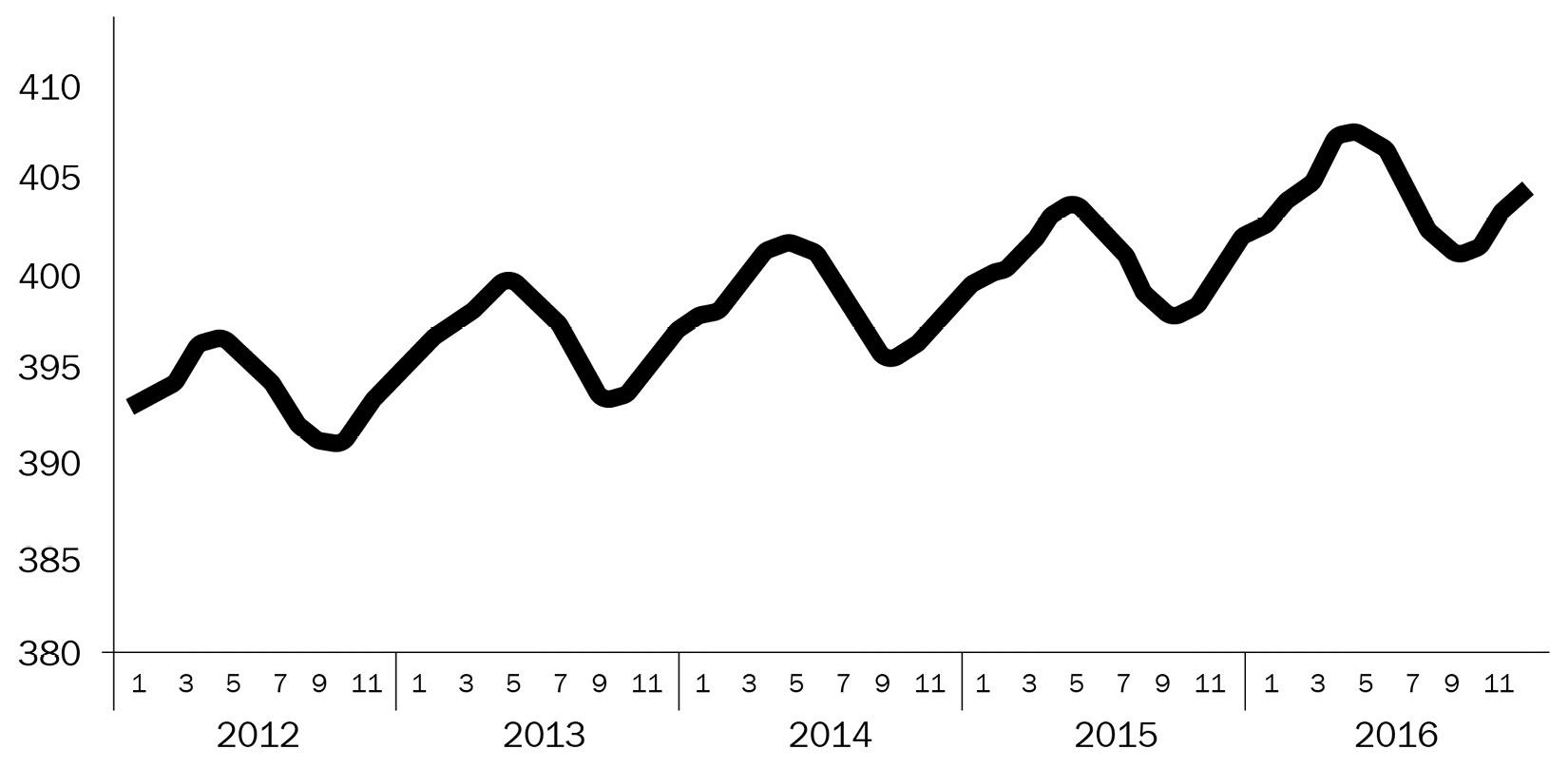
Figure 1.3 – Time series example 2: monthly carbon dioxide concentration (globally averaged from marine surface sites)
Focusing on a different series, the Monthly carbon dioxide concentration in Figure 1.3 shows a completely different pattern than the previous series. In fact, the dynamics of this monthly time series are dominated by periodic fluctuations, which are repeated consistently every year. In addition, we observe the constant growth of the level of the carbon concentration, year after year. In summary, this series shows an increasing oscillatory pattern that appears to be quite stable and, therefore, easily predictable.
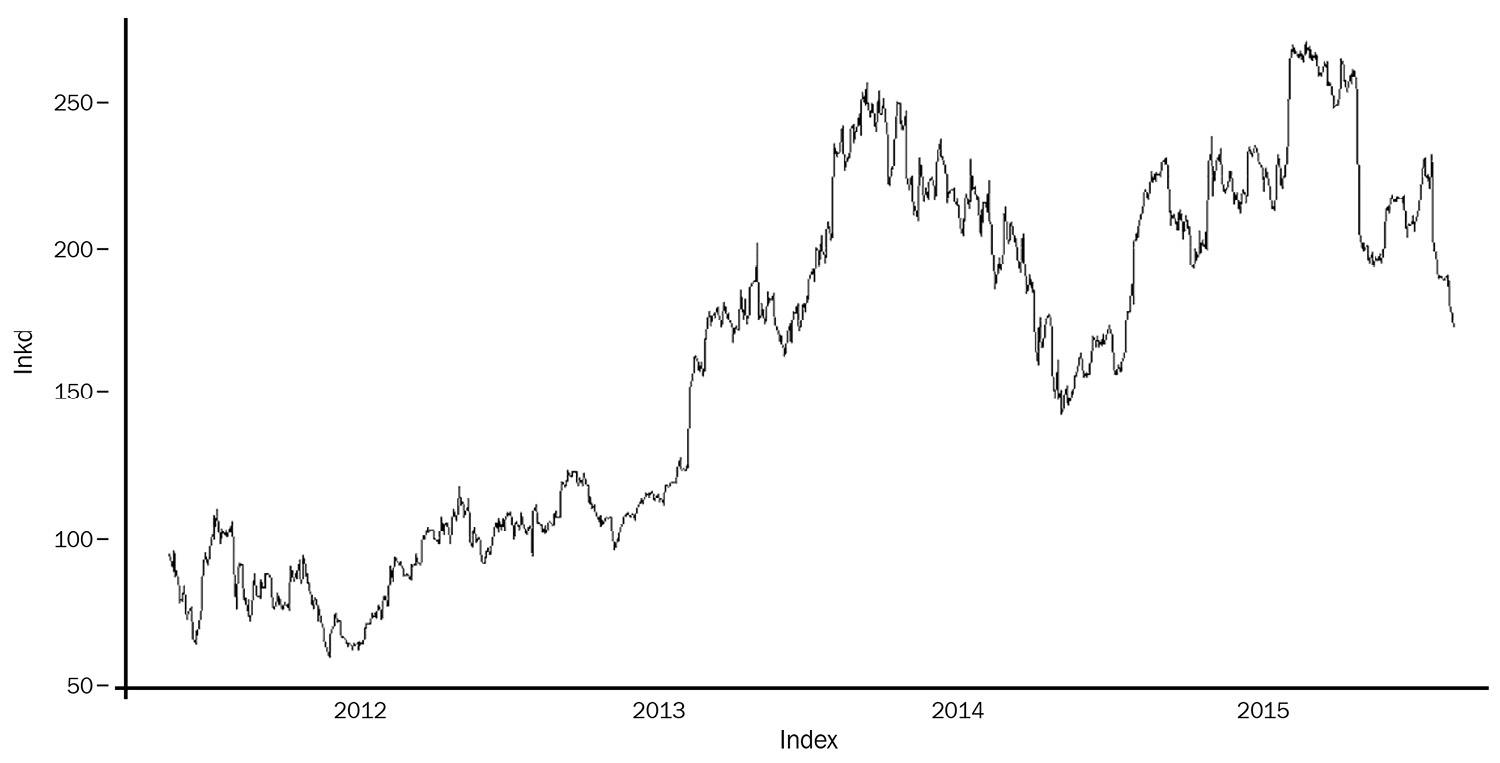
Figure 1.4 – Time series example 3: LinkedIn’s daily stock market closing price
In contrast, the evolution of the time series shown in Figure 1.4 seems to be much more unpredictable. In this case, we have daily data points of LinkedIn’s stock market closing price. The pattern during the 5 years of observation seems to be very irregular, without periodic fluctuations, with sudden changes of direction superimposed on an increasing trend in the long run.
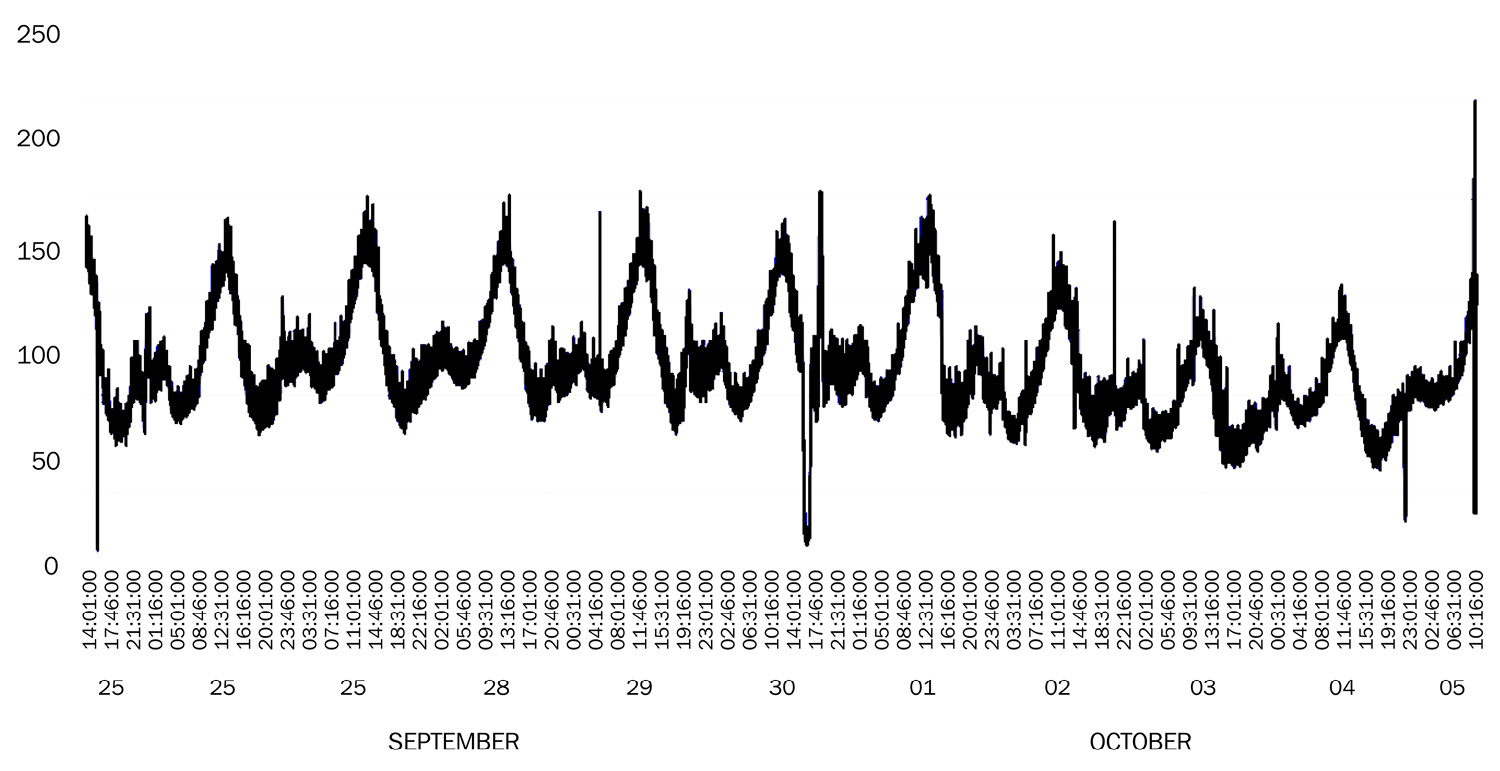
Figure 1.5 – Time series example 4: number of photos uploaded onto Instagram every minute (regional sub-sample)
Considering another example in the social media theme, we can look at Figure 1.5, in which the plot shows the Number of photos uploaded onto Instagram every minute (regional sub-sample). In this case, the granularity of the data is very high (one observation every minute) and the dynamics of the time series show both elements of regularity, such as constant fluctuations and peaks that are observed in the early afternoon of each day. At the same time, there are also discontinuities such as the presence of some anomalous observations.
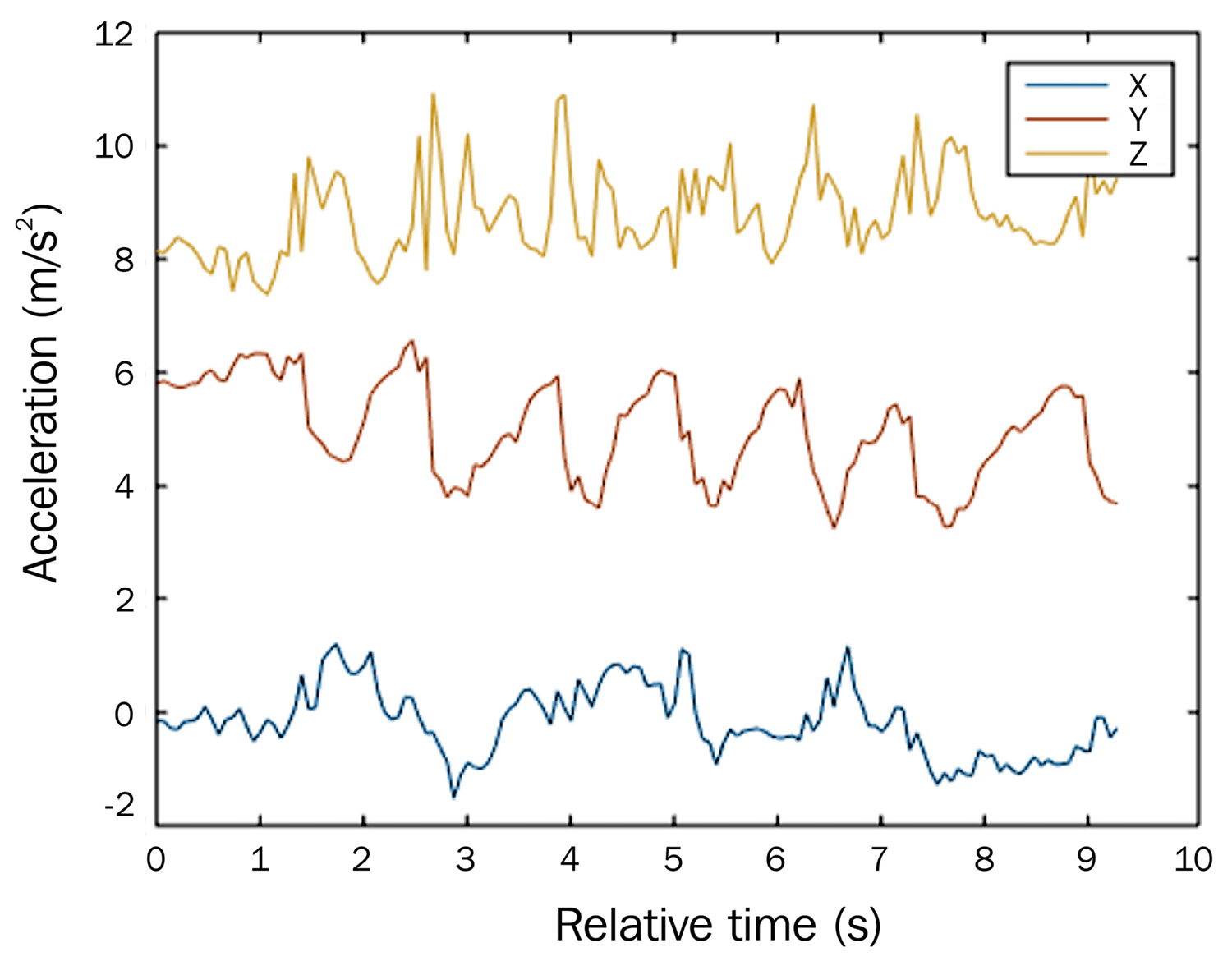
Figure 1.6 – Time series example 5: acceleration detected by smartphone sensors during a workout session (10 seconds)
Finally, the analysis of the three time series shown in Figure 1.6, highlights how, for the same phenomenon (a workout session), both regular and irregular dynamics can be observed, depending on the point of observation. In this case, the three accelerometers mounted to the wearable device show fairly constant peaks along one spatial dimension and greater irregularity on the others.
In conclusion, from the examples that we have shown in this section, we notice that time series might have characteristics that are very different from one another. Determining aspects such as the origin of the data and the reference industry, the granularity of the data, and the length of the observation period can drastically influence the dynamics of the time series, revealing really heterogeneous patterns.
































































