Solving partial differential equations numerically
Partial differential equations are differential equations that involve partial derivatives of functions in two or more variables, as opposed to ordinary derivatives in only a single variable. Partial differential equations are a vast topic, and could easily fill a series of books. A typical example of a partial differential equation is the (one-dimensional) heat equation:
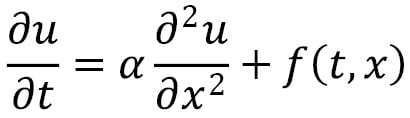
Here,  is a positive constant and
is a positive constant and  is a function. The solution to this partial differential equation is a function
is a function. The solution to this partial differential equation is a function  , which represents the temperature of a rod, occupying the
, which represents the temperature of a rod, occupying the  range
range  , at a given time
, at a given time  . To keep things simple, we will take
. To keep things simple, we will take  , which amounts to saying that no heating/cooling is applied to the system,
, which amounts to saying that no heating/cooling is applied to the system,  , and
, and  . In practice, we can rescale the problem to fix the constant
. In practice, we can rescale the problem to fix the constant  , so this is not a restrictive problem. In this example, we will use boundary conditions:
, so this is not a restrictive problem. In this example, we will use boundary conditions:
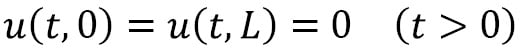
These are equivalent to saying that the ends...































































