Verifying the transformation
In-order traversal of a BST is a recursive traversal algorithm. It visits the BST tree nodes in a predefined order and always prefers to visit the left child first, then the parent itself, and finally the right child.
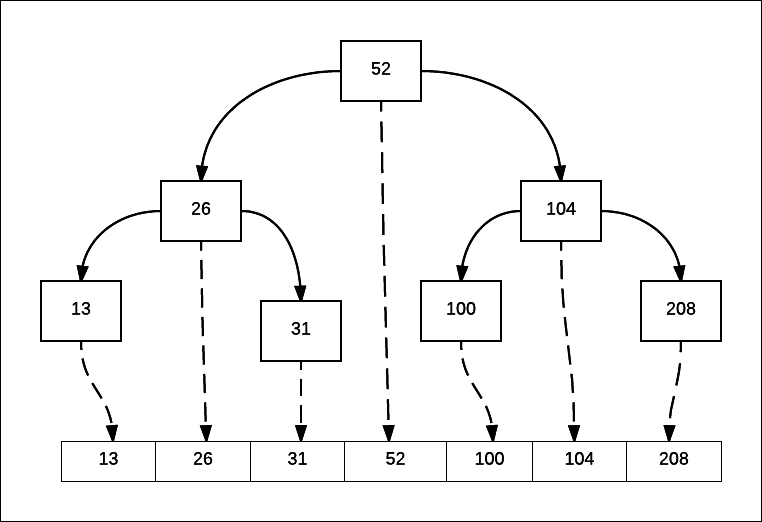
As you probably know, the visiting order is also the sorted order. If we put the values in an array as shown in the diagram, we get all the values sorted:

This traversal comes as a very useful tool to understand rotations. We can transform the tree, provided the in-order traversal visits the nodes in the same way.
The preceding diagram shows our right, left tree rotation. The numbers mark the order in which an in-order traversal would visit nodes.
The right-side-transformed tree also yields the nodes in the same order when traversed in an in-order fashion.
Drawing other rotations and verifying them in the same fashion will help you better understand the concept of rotations.












































































