Plane
A plane is a flat surface that extents infinitely in all directions. A plane has a direction, which is expressed differently based on how we represent a plane. There are three common ways to represent a plane:
Three points (not on a straight line)
A normal and a point on the plane
A normal and the distance from origin
For our plane implementation we will use the third representation, a normal, and a distance from origin:
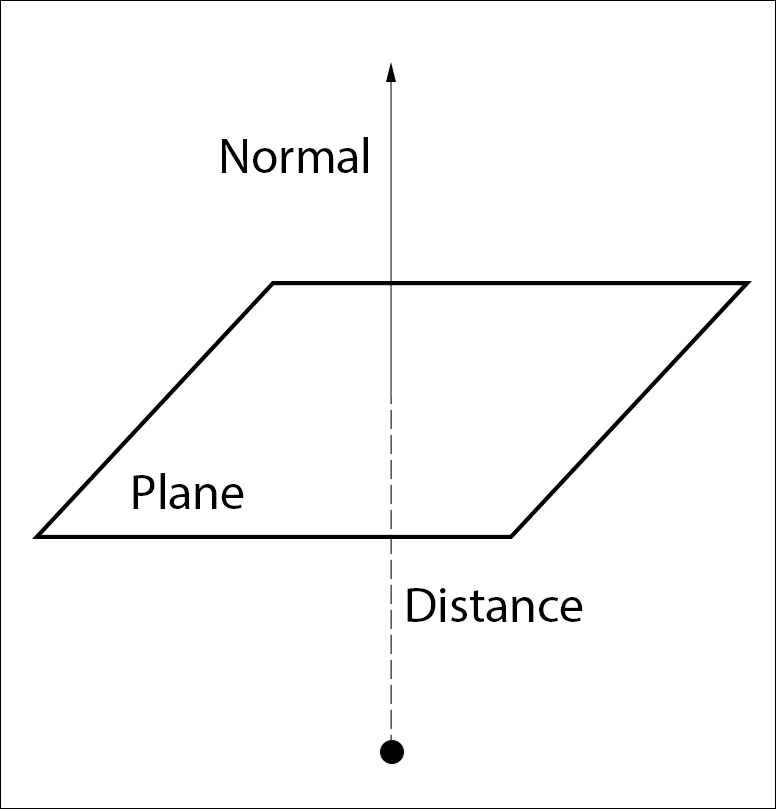
Assuming the normal of the plane is of unit length, we can use the following formula to find the distance of any point (X) from origin along the normal of the plane:
Dot(X, plane.Normal) = PointDistance // Not plane distance from origin! ^
By subtracting the distance of the plane from the distance of the point, we can check if a point is on the plane:
Dot(X, plane.Normal) - plane.Distance = 0; // Plane Equation // ^ Will always equal 0 if point is on the plane
This is called the plane equation. The preceding equation will return the following:
0if the point is on the plane...




























































