The theoretical background of the cross-entropy method
This section is optional and included for readers who are interested in why the method works. If you wish, you can refer to the original paper on the cross-entropy method, which will be given at the end of the section.
The basis of the cross-entropy method lies in the importance sampling theorem, which states this:
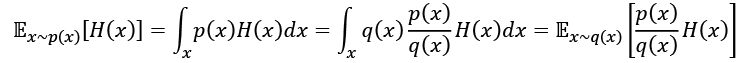
In our RL case, H(x) is a reward value obtained by some policy, x, and p(x) is a distribution of all possible policies. We don't want to maximize our reward by searching all possible policies; instead we want to find a way to approximate p(x)H(x) by q(x), iteratively minimizing the distance between them. The distance between two probability distributions is calculated by Kullback-Leibler (KL) divergence, which is as follows:
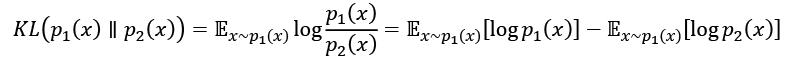
The first term in KL is called entropy and it doesn't depend on p2(x), so it could be omitted during the minimization. The second term is called cross-entropy, which is...
























































