Game AI with the Minmax Algorithm and Alpha-Beta Pruning
In the first two sections, we saw how hard it was to create a winning strategy for a simple game such as tic-tac-toe. The previous section introduced a few structures for solving search problems with the A* algorithm. We also saw that tools such as the simpleai library help us to reduce the effort we put in to describe a task with code.
We will use all of this knowledge to supercharge our game AI skills and solve more complex problems.
Search Algorithms for Turn-Based Multiplayer Games
Turn-based multiplayer games such as tic-tac-toe are similar to pathfinding problems. We have an initial state and we have a set of end states where we win the game.
The challenge with turn-based multiplayer games is the combinatorial explosion of the opponent's possible moves. This difference justifies treating turn-based games differently to a regular pathfinding problem.
For instance, in the tic-tac-toe game, from an empty board, we can select one of the nine cells and place our sign there, assuming we start the game. Let's denote this algorithm with the succ function, symbolizing the creation of successor states. Consider we have the initial state denoted by Si.
Here, we have succ(Si) returns [ S1, S2, ..., Sn ], where S1, S2, ..., Sn are successor states:
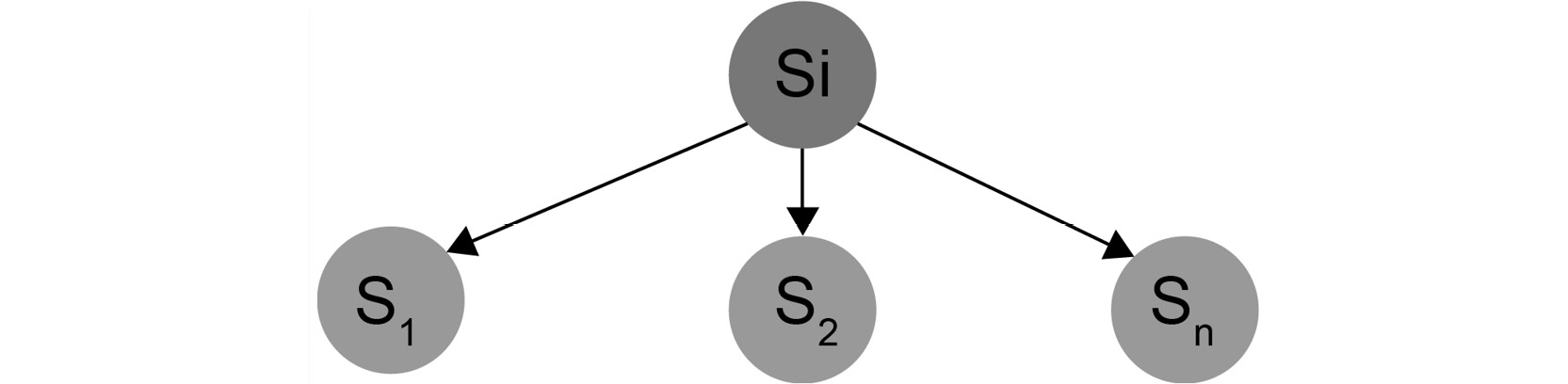
Figure 1.20: Tree diagram denoting the successor states of the function
Then, the opponent also makes a move, meaning that from each possible state, we have to examine even more states:
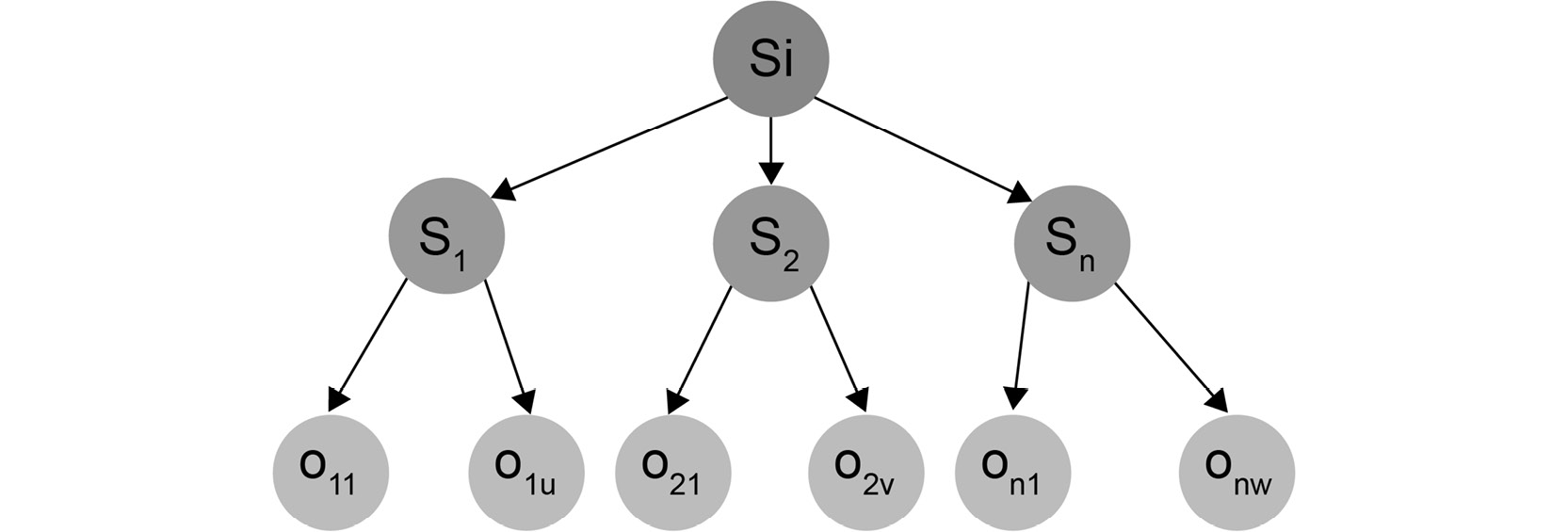
Figure 1.21: Tree diagram denoting parent-successor relationships
The expansion of possible future states stops in one of two cases:
- The game ends.
- Due to resource limitations, it is not worth explaining any more moves beyond a certain depth for the state of a certain utility.
Once we stop expanding, we have to make a static heuristic evaluation of the state. This is exactly what we did previously with the A* algorithm, when choosing the best move; however, we never considered future states.
Therefore, even though our algorithm became more and more complex, without using the knowledge of possible future states, we had a hard time detecting whether our current move would likely be a winning one or a losing one.
The only way for us to take control of the future was to change our heuristic while knowing how many games we would win, lose, or tie in the future. We could either maximize our wins or minimize our losses. We still did not dig deep enough to see whether our losses could have been avoided through smarter play on the part of the AI.
All these problems can be avoided by digging deeper into future states and recursively evaluating the utility of the branches.
To consider future states, we will learn about the Minmax algorithm and its variant, the NegaMax algorithm.























































