Singular value decomposition - SVD
Many implementations of PCA use singular value decomposition to calculate eigenvectors and eigenvalues. SVD is given by the following equation:
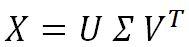
Columns of U are called left singular vectors of the data matrix, the columns of V are its right singular vectors, and the diagonal entries of
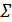
are its singular values. Left singular vectors are the eigenvectors of the covariance matrix and the diagonal element of
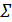
are the square roots of the eigenvalues of the covariance matrix.
Before proceeding with SVD, it would be advisable to understand a few advantages and important points about SVD:
- SVD can be applied even on rectangular matrices; whereas, eigenvalues are defined only for square matrices. The equivalent of eigenvalues obtained through the SVD method are called singular values, and vectors obtained equivalent to eigenvectors are known as singular vectors. However, as they are rectangular in nature, we need to have left singular vectors and right singular vectors...

























































