Ensembles of voting classifiers

A simpler but no less effective way to create an ensemble is based on the idea of exploiting a limited number of strong learners whose peculiarities allow them to yield better performances in particular regions of the sample space. Let's start considering a set of Nc discrete-valued classifiers f1(x), f2(x), ..., fNc(x). The algorithms are different, but they are all trained with the same dataset and output the same label set. The simplest strategy is based on a hard-voting approach:

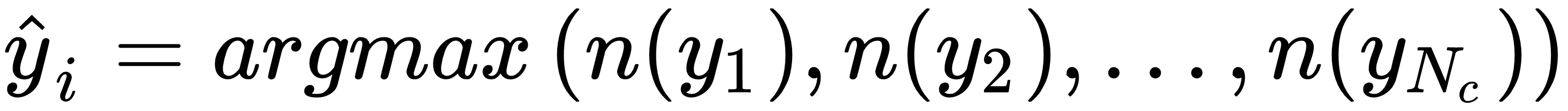
In this case, the function n(•) counts the number of estimators that output the label yi. This method is rather powerful in many cases, but has some limitations. If we rely only on a majority vote, we are implicitly assuming that a correct classification is obtained by a large number of estimators. Even if, Nc/2 + 1 votes are necessary to output a result, in many cases their number is much higher. Moreover, when k is not very large, also Nc/2 + 1 votes imply a symmetry that involves...