Motion tracking in depth

ARCore implements motion tracking using an algorithm known as visual-inertial odometry (VIO). VIO combines the identification of image features from the device's camera with internal motion sensors to track the device's orientation and position relative to where it started. By tracking orientation and position, we have the ability to understand where a device is in 6 degrees of freedom, or what we will often refer to as the device's/object's pose. Let's take a look at what a pose looks like in the following diagram:

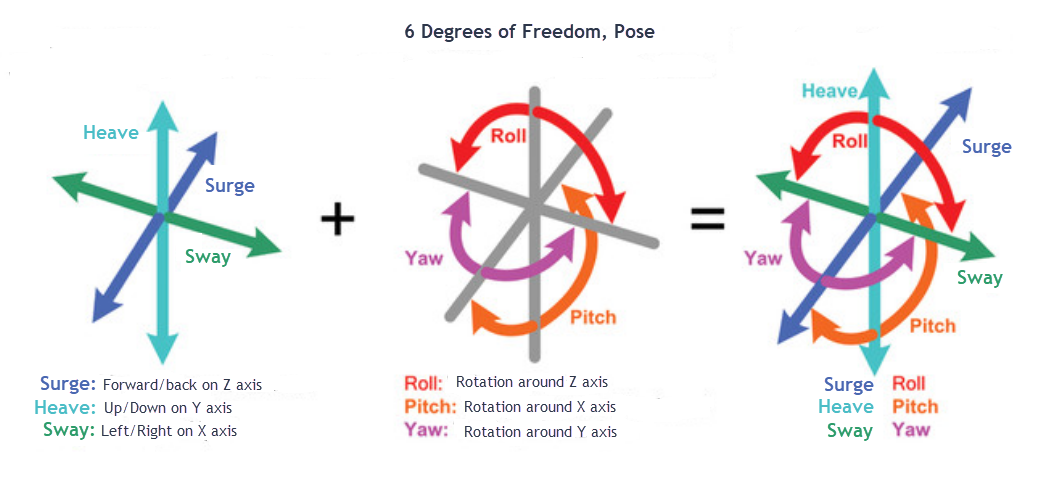
6 Degrees of Freedom, Pose

We will use the term pose frequently when identifying an object's position and orientation in 3D. If you recall from Chapter 4, ARCore on the Web, a pose can also be expressed in a mathematical notation called a matrix. We can also refer to rotation in a special form of complex math called a quaternion. Quaternions allow us to define all aspects of 3D rotation in a simple form. Again, we won't worry about the specific math here...