Approximating a quadratic regression

Given a collection of points, this recipe will try to find a best fit quadratic equation. In the following figure, the curve is a best fit quadratic regression of the points:

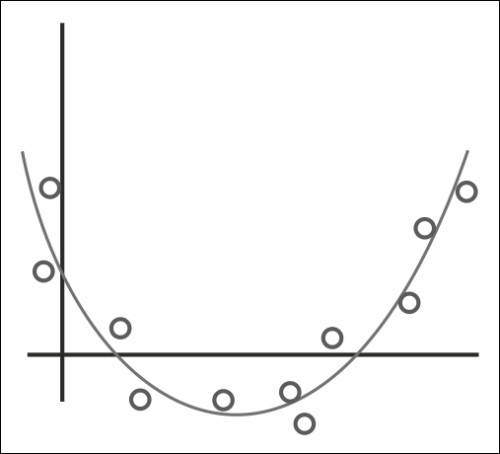
Getting ready

Install the dsp package to use Matrix.LU as follows:

$ cabal install dsp

In order to perform a quadratic regression, we will use the least square polynomial fitting algorithm described in Wolfram MathWorld available at http://mathworld.wolfram.com/LeastSquaresFittingPolynomial.html.

How to do it…

1. Import the following packages:

   import Data.Array (listArray, elems)
   import Matrix.LU (solve)

2. Implement the quadratic regression algorithm, as shown in the following code snippet:

   fit d vals = elems $ solve mat vec  
   where mat = listArray ((1,1), (d,d)) $ matrixArray
      vec = listArray (1,d) $ take d vals
      matrixArray = concat [ polys x d 
                                   | x <- [0..fromIntegral (d-1)]]
            polys x d = map (x**) [0..fromIntegral (d-1)]

3. Test out the function...