Reinforcement learning aims to create algorithms that can learn and adapt to environmental changes. This programming technique is based on the concept of receiving external stimuli that depend on the actions chosen by the agent. A correct choice will involve a reward, while an incorrect choice will lead to a penalty. The goal of the system is to achieve the best possible result, of course.
These mechanisms derive from the basic concepts of machine learning (learning from experience), in an attempt to simulate human behavior. In fact, in our mind, we activate brain mechanisms that lead us to chase and repeat what, in us, produces feelings of gratification and wellbeing. Whenever we experience moments of pleasure (food, sex, love, and so on), some substances are produced in our brains that work by reinforcing that same stimulus, emphasizing it.
Along with this mechanism of neurochemical reinforcement, an important role is represented by memory. In fact, the memory collects the experience of the subject in order to be able to repeat it in the future. Evolution has endowed us with this mechanism to push us to repeat gratifying experiences in the direction of the best solutions.
This is why we so powerfully remember the most important experiences of our life: experiences, especially those that are powerfully rewarding, are impressed in memories and condition our future explorations. Previously, we have seen that learning from experience can be simulated by a numerical algorithm in various ways, depending on the nature of the signal used for learning and the type of feedback adopted by the system.
The following diagram shows a flowchart that displays an agent's interaction with the environment in a reinforcement learning setting:
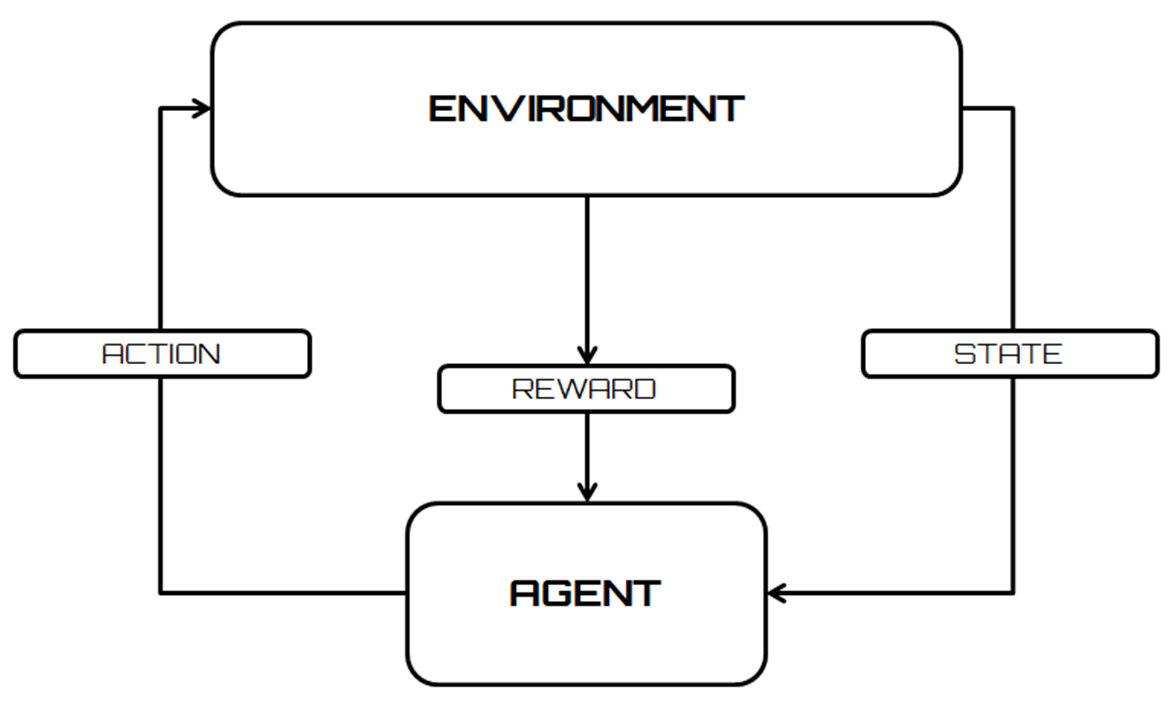
Scientific literature has taken an uncertain stance on the classification of learning by reinforcement as a paradigm. In fact, in the initial phase of the literature, it was considered a special case of supervised learning, after which it was fully promoted as the third paradigm of machine learning algorithms. It is applied in different contexts in which supervised learning is inefficient: the problems of interaction with the environment are a clear example.
The following list shows the steps to follow to correctly apply a reinforcement learning algorithm:
- Preparation of the agent
- Observation of the environment
- Selection of the optimal strategy
- Execution of actions
- Calculation of the corresponding reward (or penalty)
- Development of updating strategies (if necessary)
- Repetition of steps 2 through 5 iteratively until the agent learns the optimal strategies
Reinforcement learning is based on a theory from psychology, elaborated following a series of experiments performed on animals. In particular, Edward Thorndike (American psychologist) noted that if a cat is given a reward immediately after the execution of a behavior considered correct, then this increases the probability that this behavior will repeat itself. On the other hand, in the face of unwanted behavior, the application of a punishment decreases the probability of a repetition of the error.
On the basis of this theory, after defining a goal to be achieved, reinforcement learning tries to maximize the rewards received for the execution of the action or set of actions that allows to reach the designated goal.















































































