0

Explore Products

Best Sellers

New Releases

Books

Videos

Audiobooks

Free Learning

Game Physics Cookbook

You're reading from Game Physics Cookbook Discover over 100 easy-to-follow recipes to help you implement efficient game physics and collision detection in your games

Product type Paperback

Published in Mar 2017

Publisher Packt

ISBN-13 9781787123663

Length 480 pages

Edition 1st Edition

Languages

C++

Tools

Unity

Concepts

Game Design

Author (1):

Gabor Szauer

View More author details

Table of Contents (19) Chapters

Preface

1. Vectors FREE CHAPTER

2. Matrices

3. Matrix Transformations

4. 2D Primitive Shapes

5. 2D Collisions

6. 2D Optimizations

7. 3D Primitive Shapes

8. 3D Point Tests

9. 3D Shape Intersections

10. 3D Line Intersections

11. Triangles and Meshes

12. Models and Scenes

13. Camera and Frustum

14. Constraint Solving

15. Manifolds and Impulses

16. Springs and Joints

A. Advanced Topics

Index

Multiplication

Like a vector, there are many ways to multiply a matrix. In this chapter we will cover multiplying matrices by a scalar or by another matrix. Scalar multiplication is component wise. Given a matrix M and a scalar s, scalar multiplication is defined as follows:

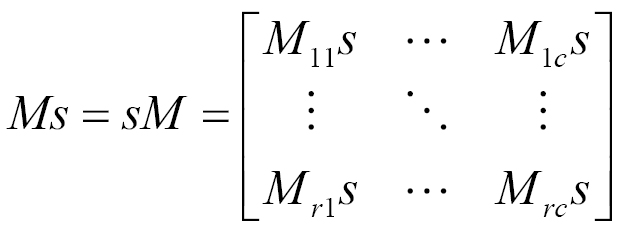
Multiplication

We can also multiply a matrix by another matrix. Two matrices, A and B, can be multiplied together only if the number of columns in A matches the number of rows in B. That is, two matrices can only be multiplied together if their inner dimensions match.

When multiplying two matrices together, the dimension of the resulting matrix will match the outer dimensions of the matrices being multiplied. If A is an Multiplication matrix and B is an matrix, the product of AB will be an matrix. We can find each element of the matrix AB with the following formula:

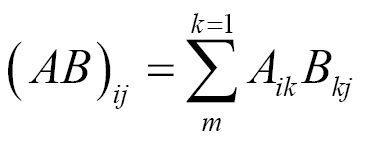
Multiplication

This operation concatenates the transformations represented by the two matrices into one matrix. Matrix multiplication is not cumulative. . However, matrix multiplication is associative...

The rest of the chapter is locked

Register for a free Packt account to unlock a world of extra content!

A free Packt account unlocks extra newsletters, articles, discounted offers, and much more. Start advancing your knowledge today.

Unlock this book and the full library FREE for 7 days

Get unlimited access to 7000+ expert-authored eBooks and videos courses covering every tech area you can think of

Start free trial

Renews at €18.99/month. Cancel anytime

Authors (1)

Gabor Szauer

Gabor Szauer

Gabor Szauer has been making games since 2010. He graduated from Full Sail University in 2010 with a bachelor's degree in game development. Gabor maintains an active Twitter presence, and maintains a programming-oriented game development blog. Gabor's previously published books are Game Physics Programming Cookbook and Lua Quick Start Guide, both published by Packt.

See other products by Gabor Szauer

Other recommended products

Related to this chapter

Hands-On C++ Game Animation Programming

Hands-On C++ Game Animation Programming

Game Animation Programming is a comprehensive guide to learning everything needed to get an optimized, production ready animation system up and running. It covers all the concepts starting from understanding OpenGL, the math required for animations, how to write a robust animation system, right through advanced animation methods.

Jun 2020 12h 16m

Hands-On C++ Game Animation Programming

Hands-On C++ Game Animation Programming

Game Animation Programming is a comprehensive guide to learning everything needed to get an optimized, production ready animation system up and running. It covers all the concepts starting from understanding OpenGL, the math required for animations, how to write a robust animation system, right through advanced animation methods.

Jun 2020 12h 16m

Hands-On C++ Game Animation Programming

Hands-On C++ Game Animation Programming

Game Animation Programming is a comprehensive guide to learning everything needed to get an optimized, production ready animation system up and running. It covers all the concepts starting from understanding OpenGL, the math required for animations, how to write a robust animation system, right through advanced animation methods.

Jun 2020 12h 16m

Hands-On C++ Game Animation Programming

Hands-On C++ Game Animation Programming

Game Animation Programming is a comprehensive guide to learning everything needed to get an optimized, production ready animation system up and running. It covers all the concepts starting from understanding OpenGL, the math required for animations, how to write a robust animation system, right through advanced animation methods.

Jun 2020 12h 16m

C++ Game Development By Example

C++ Game Development By Example

This book will get you up to speed with the specifics of making games look and feel great, by using modern animation and rendering techniques with the integration of great physics libraries for an improved and realistic user experience.

May 2019 14h 0m

C++ Game Development By Example

C++ Game Development By Example

This book will get you up to speed with the specifics of making games look and feel great, by using modern animation and rendering techniques with the integration of great physics libraries for an improved and realistic user experience.

May 2019 14h 0m

C++ Game Development By Example

C++ Game Development By Example

This book will get you up to speed with the specifics of making games look and feel great, by using modern animation and rendering techniques with the integration of great physics libraries for an improved and realistic user experience.

May 2019 14h 0m

C++ Game Development By Example

C++ Game Development By Example

This book will get you up to speed with the specifics of making games look and feel great, by using modern animation and rendering techniques with the integration of great physics libraries for an improved and realistic user experience.

May 2019 14h 0m

C++ Game Development By Example

C++ Game Development By Example

This book will get you up to speed with the specifics of making games look and feel great, by using modern animation and rendering techniques with the integration of great physics libraries for an improved and realistic user experience.

May 2019 14h 0m

C++ Game Development By Example

C++ Game Development By Example

This book will get you up to speed with the specifics of making games look and feel great, by using modern animation and rendering techniques with the integration of great physics libraries for an improved and realistic user experience.

May 2019 14h 0m

C++ Game Development By Example

C++ Game Development By Example

This book will get you up to speed with the specifics of making games look and feel great, by using modern animation and rendering techniques with the integration of great physics libraries for an improved and realistic user experience.

May 2019 14h 0m

Personalised recommendations for you

Based on your interests and search pattern

Realizing 3D Animation in Blender

Realizing 3D Animation in Blender

Learn Blender and animation at the same time! With clearly explained exercises, insightful commentary, and a focus on animation, this book has everything you need to start animating with the world's most advanced free software for 3D content creation.

Jul 2024 15h 12m

Realizing 3D Animation in Blender

Realizing 3D Animation in Blender

Learn Blender and animation at the same time! With clearly explained exercises, insightful commentary, and a focus on animation, this book has everything you need to start animating with the world's most advanced free software for 3D content creation.

Jul 2024 15h 12m

Realizing 3D Animation in Blender

Realizing 3D Animation in Blender

Learn Blender and animation at the same time! With clearly explained exercises, insightful commentary, and a focus on animation, this book has everything you need to start animating with the world's most advanced free software for 3D content creation.

Jul 2024 15h 12m

Realizing 3D Animation in Blender

Realizing 3D Animation in Blender

Learn Blender and animation at the same time! With clearly explained exercises, insightful commentary, and a focus on animation, this book has everything you need to start animating with the world's most advanced free software for 3D content creation.

Jul 2024 15h 12m

Realizing 3D Animation in Blender

Realizing 3D Animation in Blender

Learn Blender and animation at the same time! With clearly explained exercises, insightful commentary, and a focus on animation, this book has everything you need to start animating with the world's most advanced free software for 3D content creation.

Jul 2024 15h 12m

Realizing 3D Animation in Blender

Realizing 3D Animation in Blender

Learn Blender and animation at the same time! With clearly explained exercises, insightful commentary, and a focus on animation, this book has everything you need to start animating with the world's most advanced free software for 3D content creation.

Jul 2024 15h 12m

Realizing 3D Animation in Blender

Realizing 3D Animation in Blender

Learn Blender and animation at the same time! With clearly explained exercises, insightful commentary, and a focus on animation, this book has everything you need to start animating with the world's most advanced free software for 3D content creation.

Jul 2024 15h 12m

Unity 2022 by Example

Unity 2022 by Example

This book will introduce you to C# concepts and programming patterns in Unity that will help you solve common problems. After working on a range of 2D, 3D, AR, and VR game projects, you'll be able to confidently build playable and commercial games.

Jun 2024 19h 52m

Unity 2022 by Example

Unity 2022 by Example

This book will introduce you to C# concepts and programming patterns in Unity that will help you solve common problems. After working on a range of 2D, 3D, AR, and VR game projects, you'll be able to confidently build playable and commercial games.

Jun 2024 19h 52m

Unity 2022 by Example

Unity 2022 by Example

This book will introduce you to C# concepts and programming patterns in Unity that will help you solve common problems. After working on a range of 2D, 3D, AR, and VR game projects, you'll be able to confidently build playable and commercial games.

Jun 2024 19h 52m

Unity 2022 by Example

Unity 2022 by Example

This book will introduce you to C# concepts and programming patterns in Unity that will help you solve common problems. After working on a range of 2D, 3D, AR, and VR game projects, you'll be able to confidently build playable and commercial games.

Jun 2024 19h 52m

Unity 2022 by Example

Unity 2022 by Example

This book will introduce you to C# concepts and programming patterns in Unity that will help you solve common problems. After working on a range of 2D, 3D, AR, and VR game projects, you'll be able to confidently build playable and commercial games.

Jun 2024 19h 52m