Multiple regression
More often than not, we want to include not just one, but multiple predictors (independent variables) in our predictive models. Luckily, linear regression can easily accommodate us! The technique? Multiple regression.
By giving each predictor its very own beta coefficient in a linear model, the target variable gets informed by a weighted sum of its predictors. For example, a multiple regression using two predictor variables looks like this:
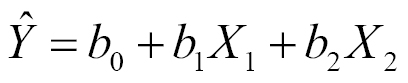
Now, instead of estimating two coefficients ( b0 and b1), we are estimating three: the intercept, the slope of the first predictor, and the slope of the second predictor.
Before explaining further, let's perform a multiple regression predicting gas mileage from weight and horsepower, using the following code:
model <- lm(mpg ~ wt + hp, data=mtcars)
summary(model)
Call:
lm(formula = mpg ~ wt + hp, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.941 -1.600 -0.182 1.050 5.854
Coefficients...


























































