8.1 What are elliptic curves?

Historically, elliptic curves are rooted in so-called Diophantine equations, named after ancient Greek mathematician Diophantus of Alexandria. Diophantine equations are polynomial equations in two or more unknowns for which only integer solutions are of interest.

In the 19th century, these studies became more formalized and were extended to so called algebraic curves, which are the set of zeros of a polynomial of two variables in a plane. Circles, as defined as the zeros of

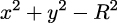
and ellipses, defined as the zeros of

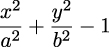
are the most common examples of algebraic curves. However, elliptic curves are not ellipses. They arose from the study of so-called elliptic integrals, by which the arc length of ellipses is computed, and were intensively studied by pure mathematicians in the 19th and early 20th century. They are characterized by their amazing property of possessing a way to add curve points, so that the result is another point on the curve.

In 1985, Victor Miller...