Designing complex if...elif chains
In most cases, our scripts will involve a number of choices. Sometimes the choices are simple, and we can judge the quality of the design with a glance at the code. In other cases, the choices are more complex, and it's not easy to determine whether or not our if statements are designed properly to handle all of the conditions.
In the simplest case, we have one condition, C, and its inverse, ¬C` . These are the two conditions for an if...else statement. One condition, C, is stated in the if clause, the other condition, C's inverse, is implied in else.
This is the Law of the Excluded Middle: we're claiming there's no missing alternative between the two conditions, C and ¬C. For a complex condition, though, this isn't always true.
If we have something like:
if weather == RAIN and plan == GO_OUT:
bring("umbrella")
else:
bring("sunglasses")
It may not be immediately obvious, but we've omitted a number of possible alternatives. The weather and plan variables have four different combinations of values. One of the conditions is stated explicitly, the other three are assumed:
weather == RAINandplan == GO_OUT. Bringing an umbrella seems right.weather != RAINandplan == GO_OUT. Bringing sunglasses seems appropriate.weather == RAINandplan != GO_OUT. If we're staying in, then neither accessory seems right.weather != RAINandplan != GO_OUT. Again, the accessory question seems moot if we're not going out.
How can we be sure we haven't missed anything?
Getting ready
Let's look at a concrete example of an if...elif chain. In the casino game of Craps, there are a number of rules that apply to a roll of two dice. These rules apply on the first roll of the game, called the come-out roll:
- 2, 3, or 12 is Craps, which is a loss for all bets placed on the pass line
- 7 or 11 is a winner for all bets placed on the pass line
- The remaining numbers establish a point
Many players place their bets on the pass line. We'll use this set of three conditions as an example for looking at this recipe because it has a potentially vague clause in it.
How to do it...
When we write an if statement, even when it appears trivial, we need to be sure that all conditions are covered.
- Enumerate the conditions we know. In our example, we have three rules: (2, 3, 12), (7, 11), and a vague statement of "the remaining numbers." This forms a first draft of the
ifstatement. - Determine the universe of all possible alternatives. For this example, there are 11 alternative outcomes: the numbers from 2 to 12, inclusive.
- Compare the conditions, C, with the universe of alternatives, U. There are three possible outcomes of this comparison:
- More conditions than are possible in the universe of alternatives,
 . The most common cause is failing to completely enumerate all possible alternatives in the universe. We might, for example, have modeled dice using 0 to 5 instead of 1 to 6. The universe of alternatives appears to be the values from 0 to 10, yet there are conditions for 11 and 12.
. The most common cause is failing to completely enumerate all possible alternatives in the universe. We might, for example, have modeled dice using 0 to 5 instead of 1 to 6. The universe of alternatives appears to be the values from 0 to 10, yet there are conditions for 11 and 12. - Gaps in the conditions,
 . There are one or more alternatives without a condition. The most common cause is failing to fully understand the various conditions. We might, for example, have enumerated the vales as two tuples instead of sums. (1, 1), (1, 2), (2, 1), and (6, 6) have special rules. It's possible to miss a condition like this and have a condition untested by any clause of the
. There are one or more alternatives without a condition. The most common cause is failing to fully understand the various conditions. We might, for example, have enumerated the vales as two tuples instead of sums. (1, 1), (1, 2), (2, 1), and (6, 6) have special rules. It's possible to miss a condition like this and have a condition untested by any clause of the ifstatement. - Match between conditions and the universe of alternatives,
 . This is ideal. The universe of all possible alternatives matches of all the conditions in the
. This is ideal. The universe of all possible alternatives matches of all the conditions in the ifstatement.
- More conditions than are possible in the universe of alternatives,
The first outcome is a rare problem where the conditions in our code seem to describe too many alternative outcomes. It helps to uncover these kinds of problems as early as possible to permit rethinking the design from the foundations. Often, this suggests the universe of alternatives is not fully understood; either we wrote too many conditions or failed to identify all the alternative outcomes.
A more common problem is to find a gap between the designed conditions in the draft if statement and the universe of possible alternatives. In this example, it's clear that we haven't covered all of the possible alternatives. In other cases, it takes some careful reasoning to understand the gap. Often, the outcome of our design effort is to replace any vague or poorly defined terms with something much more precise.
In this example, we have a vague term, which we can replace with something more specific. The term remaining numbers appears to be the list of values (4, 5, 6, 8, 9, 10). Supplying this list removes any possible gaps and doubts.
The goal is to have the universe of known alternatives match the collection of conditions in our if statement. When there are exactly two alternatives, we can write a condition expression for one of the alternatives. The other condition can be implied; a simple if and else will work.
When we have more than two alternatives, we'll have more than two conditions. We need to use this recipe to write a chain of if and elif statements, one statement per alternative:
- Write an
if...elif...elifchain that covers all of the known alternatives. For our example, it will look like this:dice = die_1 + die_2 if dice in (2, 3, 12): game.craps() elif dice in (7, 11): game.winner() elif dice in (4, 5, 6, 8, 9, 10): game.point(die) - Add an
elseclause that raises an exception, like this:else: raise Exception('Design Problem')
This extra else gives us a way to positively identify when a logic problem is found. We can be sure that any design error we made will lead to a conspicuous problem when the program runs. Ideally, we'll find any problems while we're unit testing.
In this case, it is clear that all 11 alternatives are covered by the if statement conditions. The extra else can't ever be used. Not all real-world problems have this kind of easy proof that all the alternatives are covered by conditions, and it can help to provide a noisy failure mode.
How it works...
Our goal is to be sure that our program always works. While testing helps, we can still have the same wrong assumptions when doing design and creating test cases.
While rigorous logic is essential, we can still make errors. Further, someone doing ordinary software maintenance might introduce an error. Adding a new feature to a complex if statement is a potential source of problems.
This else-raise design pattern forces us to be explicit for each and every condition. Nothing is assumed. As we noted previously, any error in our logic will be uncovered if the exception gets raised.
The else-raise design pattern doesn't have a significant performance impact. A simple else clause is slightly faster than an elif clause with a condition. However, if we think that our application performance depends in any way on the cost of a single expression, we've got more serious design problems to solve. The cost of evaluating a single expression is rarely the costliest part of an algorithm.
Crashing with an exception is sensible behavior in the presence of a design problem. An alternative is to write a message to an error log. However, if we have this kind of logic gap, the program should be viewed as fatally broken. It's important to find and fix this as soon as the problem is known.
There's more...
In many cases, we can derive an if...elif...elif chain from an examination of the desired post condition at some point in the program's processing. For example, we may need a statement that establishes something simple, like: m is equal to the larger of a or b.
(For the sake of working through the logic, we'll avoid Python's handy m = max(a, b), and focus on the way we can compute a result from exclusive choices.)
We can formalize the final condition like this:
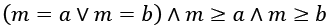
We can work backward from this final condition, by writing the goal as an assert statement:
# do something
assert (m == a or m == b) and m >= a and m >= b
Once we have the goal stated, we can identify statements that lead to that goal. Clearly assignment statements like m = a or m = b would be appropriate, but each of these works only under certain conditions.
Each of these statements is part of the solution, and we can derive a precondition that shows when the statement should be used. The preconditions for each assignment statement are the if and elif expressions. We need to use m = a when a >= b; we need to use m = b when b >= a. Rearranging logic into code gives us this:
if a >= b:
m = a
elif b >= a:
m = b
else:
raise Exception('Design Problem')
assert (m == a or m == b) and m >= a and m >= b
Note that our universe of conditions, U = {a ≥ b, b ≥ a}, is complete; there's no other possible relationship. Also notice that in the edge case of a = b, we don't actually care which assignment statement is used. Python will process the decisions in order, and will execute m = a. The fact that this choice is consistent shouldn't have any impact on our design of if...elif...elif chains. We should always write the conditions without regard to the order of evaluation of the clauses.
See also
- This is similar to the syntactic problem of a dangling else. See http://www.mathcs.emory.edu/~cheung/Courses/561/Syllabus/2-C/dangling-else.html
- Python's indentation removes the dangling else syntax problem. It doesn't remove the semantic issue of trying to be sure that all conditions are properly accounted for in a complex
if...elif...elifchain.



























































