Polynomial regression is a technique based on a trick that allows the use of linear models even when the dataset has strong non-linearities. The idea is to add some extra variables computed from the existing ones and using (in this case) only polynomial combinations:
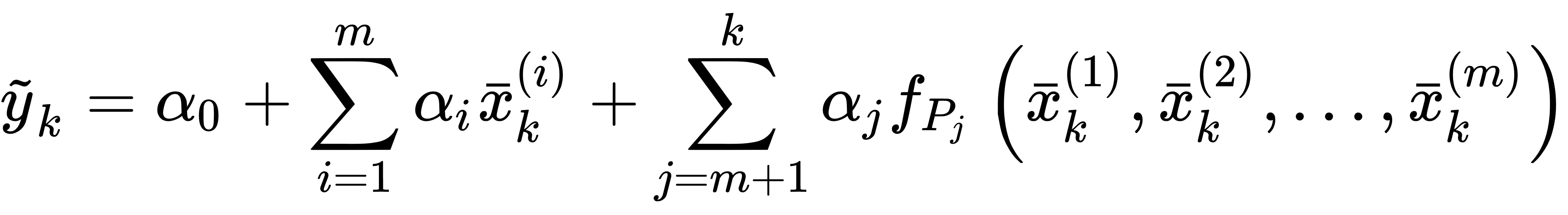
In the previous expression, every fPj(•) is a polynomial function of a single feature. For example, with two variables, it's possible to extend to a second-degree problem by transforming the initial vector (whose dimension is equal to m) into another one with higher dimensionality (whose dimension is k > m):
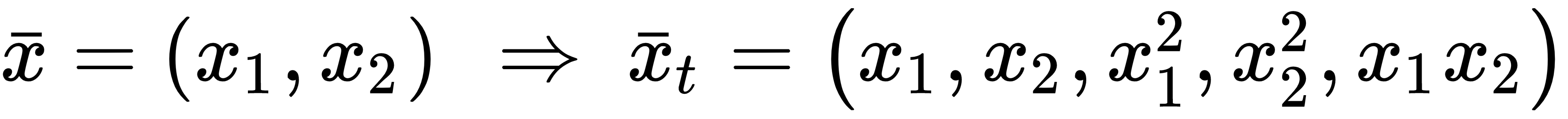
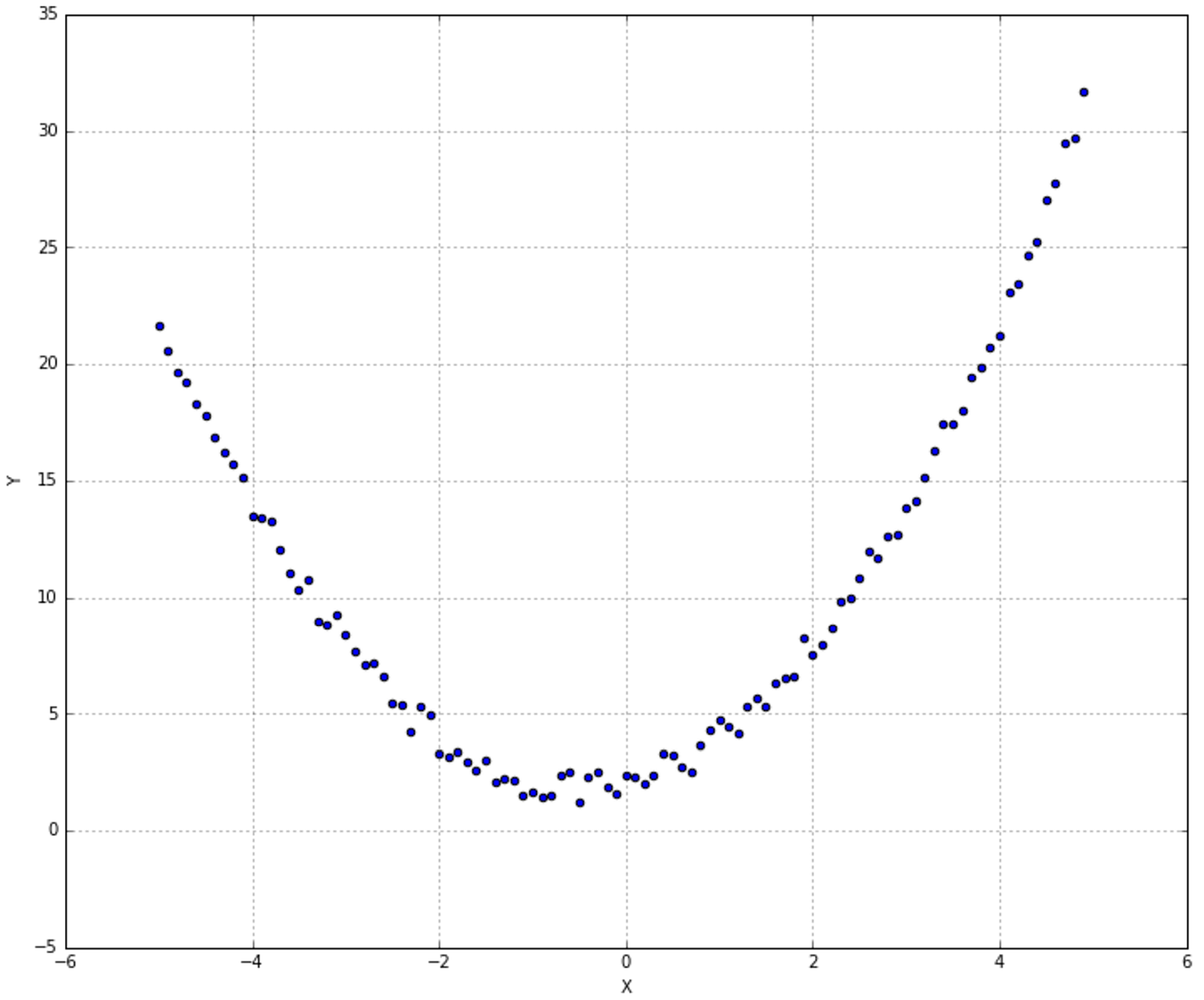
In this case, the model remains externally linear, but it can capture internal non-linearities. To show how scikit-learn implements this technique, let's consider the dataset shown in the following graph: