Let's consider two probabilistic events, A and B. We can correlate the marginal probabilities P(A) and P(B) with the conditional probabilities P(A|B) and P(B|A), using the product rule:
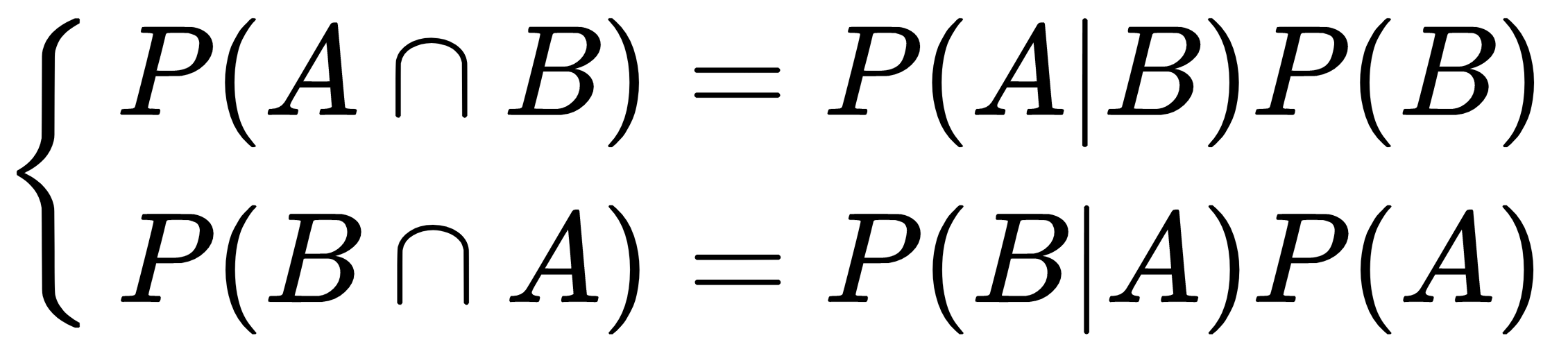
Considering that the intersection is commutative, the first members are equal, so we can derive Bayes' theorem:
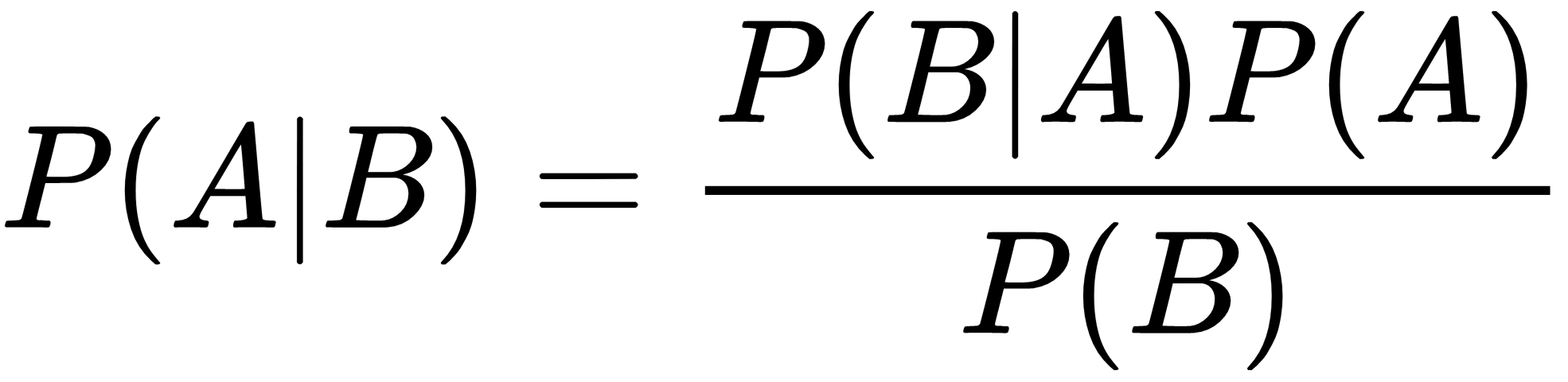
In the general discrete case, the formula can be re-expressed considering all possible outcomes for the random variable A:
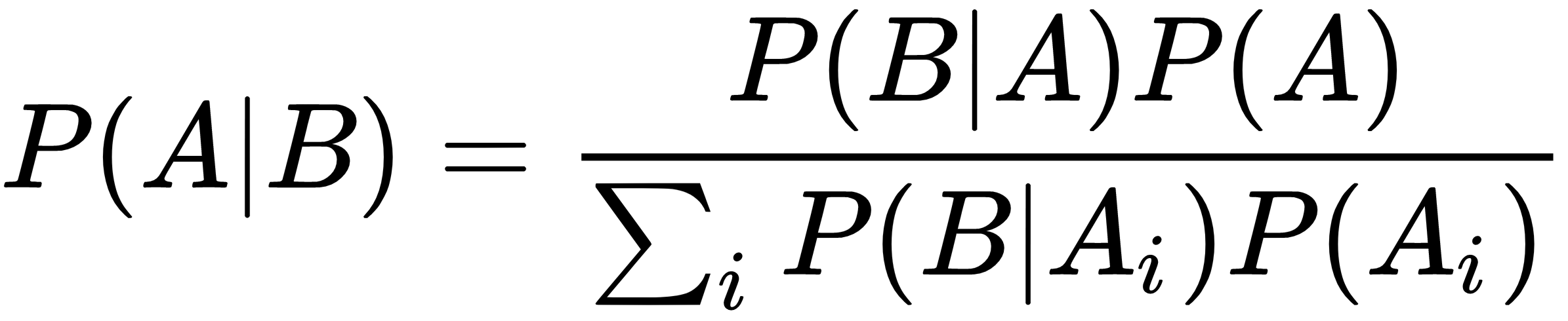
As the denominator is a normalization factor, the formula is often expressed as a proportionality relationship:
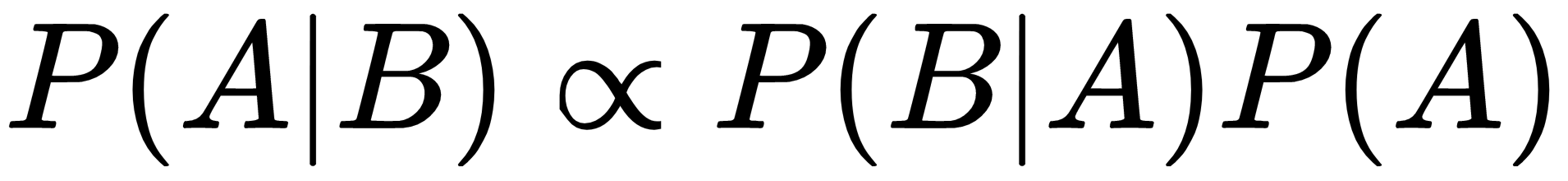
This formula has very deep philosophical implications, and it's a fundamental element of statistical learning. First of all, let's consider the marginal probability, P(A). This is normally a value that determines how probable a target event is, such as P(Spam) or P(Rain). As there are no other elements, this kind...











































































