Mixture of Bernoulli

The mixture of Bernoulli is another interesting problem. As we saw earlier, the graphical model to represent such a model is always the same. Only the probability distribution functions associated to each node change compared to the previous example. The mixture of Bernoulli finds applications in particular in analyzing black and white images, where an image is made of one Bernoulli variable for each pixel. Then the goal is to classify an image, that is, to say which value of the latent variable produced it, given some observed pixels.

For example, the following (very stylized) figure represents the letter A:

In a real application, we would use more pixels. But the idea of the application is to associate the value of pixels to each value of the latent variable, each one representing a different letter. This is a simple model for character recognition.

The distribution of a Bernoulli variable is:

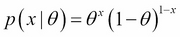
Now, let's say we have D Bernoulli variables. Each Bernoulli variable is parameterized...