Log Transformation
The most common technique to correct for skewed distribution is to find an appropriate mathematical function that has an inverse. One such function is a log, represented as follows:
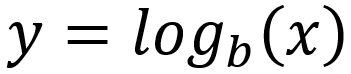
In other words,  is the
is the  of
of  to the base
to the base  . The inverse, to find the
. The inverse, to find the  , can be computed as follows:
, can be computed as follows:
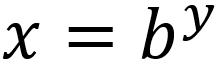
This transformation gives the ability to handle the skewness in the data; at the same time, the original value can be easily computed once the model is built. The most popular log transformation is the natural  , where
, where  is the mathematical constant
is the mathematical constant  , which equals roughly 2.71828.
, which equals roughly 2.71828.
One useful property of the log function is that it handles the data skewness elegantly. For example, the following code demonstrates the difference between log(10000) and log(1000000) as just 4.60517. The number  is 100 times bigger than
is 100 times bigger than  . This reduces the skewness that we otherwise let the model handle, which it might not do sufficiently.
. This reduces the skewness that we otherwise let the model handle, which it might not do sufficiently.
#Natural Log log(10000) ## [1] 9.21034 # 10 times bigger value log(100000) ## [1] 11...












































































