For each observation used in a model, there are three relevant metrics that help us to understand the impact of it on the estimated coefficients. The first metric is the leverage: the potential of an observation to change the estimated coefficient. The second relevant metric is the residual, which is the difference between the prediction and the observed value. Finally, the third is the influence, which can be thought of as the product between the leverage and the residual(ness). Another way of looking at this would be to think of the leverage as the horizontal distance between an observation and the rest of the regression line and the residual as the vertical distance between the observation and the regression line. Essentially, we can have four cases, as depicted in the following graphs:
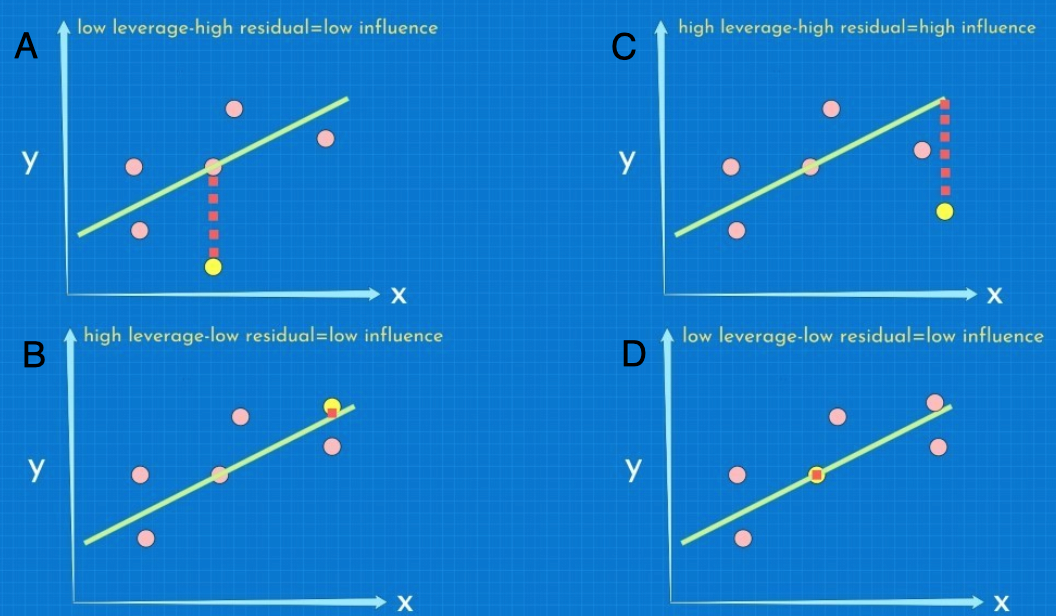
In A, we have an observation with a high residual...


























































